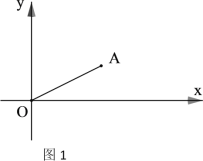
【题目】如图1,在平面直角坐标系中,已知A(a,b),且a.b满足![]() ,
,
(1)求A点的坐标及线段OA的长度;(2)点P为x轴正半轴上一点,且△AOP是等腰三角形,求P点的坐标;
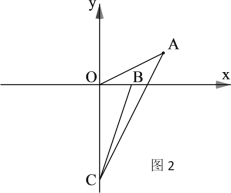
(3)如图2,若B(1,0),C(0,-3),试确定∠ACO+∠BCO的值是否发生变化,若不变,求其值;若变化,请求出变化范围。
参考答案:
【答案】(1)![]() ;(2)P(
;(2)P(![]() ,0)或P(4,0)、P(
,0)或P(4,0)、P(![]() ,0);(3)45.
,0);(3)45.
【解析】
(1)先由二次根式有意义的条件得出a的值,再代入等式得出b的值,从而得出点A的坐标,继而利用两点间的距离公式可得OA的长;
(2)分OA=OP、AO=AP、PO=PA三种情况,利用等腰三角形的性质逐一求解可得;
(3)在x轴负半轴上取一点,使得OD=OB=1,知点B与点D关于y轴对称,据此得∠BCO=∠DCO,根据两点间的距离公式知AD2=10,CD2=10,AC2=20,依据勾股定理逆定理判断出△ACD是等腰直角三角形,利用∠ACO+∠BCO=∠ACO+∠DCO=∠ACD可得答案.
解:
(1)∵![]() ,
,
∴a=2,
则b=1,
∴A(2,1),
则OA=![]() =
=![]() ;
;
(2)当OA=OP时,P(![]() ,0);
,0);
当AO=AP时,如图1,作AH⊥x轴于点H,
则OH=PH=2,
∴OP=4,
∴P(4,0);
当P′O=P′A时,设P′O=P′A=x,则P′H=2-x,

由AP′2=P′H2+AH2得(2-x)2+12=x2,
解得:x=![]() ,
,
∴P(![]() ,0).
,0).
(3)如图2,在x轴负半轴上取一点,使得OD=OB=1,

则点B与点D关于y轴对称,
∴∠BCO=∠DCO,
∵A(2,1),D(-1,0),C(0,-3),
∴AD2=32+12=10,CD2=12+32=10,AC2=22+42=20,
∴AD2+CD2=AC2,且AD=CD,
∴△ACD是等腰直角三角形,
则∠ACO+∠BCO=∠ACO+∠DCO=∠ACD=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, ∠B、∠D的两边分别平行。
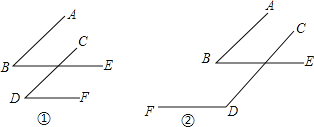
(1)在图1中,∠B与∠D的数量关系是 ;在图2中,∠B与∠FDC的数量关系是 ;
(2)用一句话归纳的结论为: ;
(3)已知∠α的两边与∠β的两边分别平行,并且∠α比∠β的3倍少
 ,求∠α、∠β的度数.
,求∠α、∠β的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若
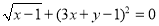 ,求
,求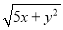 的值。
的值。(2)已知5x+19的立方根是4,2y-3的算术平方根是3,求3x-
 y的平方根。
y的平方根。(3)设a、b、c都是实数,且满足
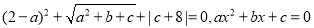 ,求式子x
,求式子x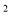 +2x的算术平方根.
+2x的算术平方根. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC为等边三角形
(1)若D为△ABC外一点,满足∠CDB=30,求证:
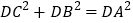
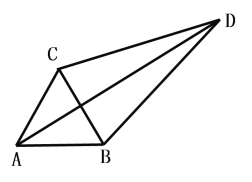
(2)若D为△ABC内一点,DC=3,DB=4,DA=5,求∠CDB的度数
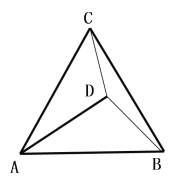
(3)若D为△ABC内一点,DA=4,DB=
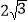 ,DC=
,DC=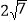 则AB= (直接写出答案)
则AB= (直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)
 ;
;(2)90°-(23°16′+17°23′)+19°40′÷6
(3)
 ;
;(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市体育中考项目分为必测项目和选测项目,必测项目为:跳绳、立定跳远;选测项目为50米、实心球、踢毽子三项中任选一项.
(1)每位考生将有 种选择方案;
(2)用画树状图或列表的方法求小颖和小华将选择同种方案的概率.
相关试题

