【题目】如图,D是AB上一点,DF交AC于点E,FC∥AB,则下列结论错误的是( )

A. 若AE=CE,则DE=FE B. 若DE=FE,则AE=CE
C. 若BC=CF,则AD=CF D. 若AD=CF,则DE=FE
参考答案:
【答案】C
【解析】由题目已知条件、结合每个选项分别证得三角形全等即可判断得出答案.
∵AB∥FC,
∴∠A=∠ACF,∠ADE=∠F,
当AE=CE时,利用AAS则可证得△ADE≌△CFE,则有DE=EF,故A选项说法是正确的,不符合题意,
当DE=FE时,同理可证得△ADE≌△CFE,则有AE=CE,故B选项说法是正确的,不符合题意,
当BC=CF时,无法证明△ADE≌△CFE,即无法得出AD=CF,故C说法是错误的,符合题意,
当AD=CF时,利用ASA则可证得△ADE≌△CFE,则有DE=FE,故D选项是正确的,不符合题意,
故选:C.
-
科目: 来源: 题型:
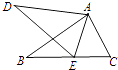
查看答案和解析>>【题目】如图,∠DAB=∠CAE,要使△ABC∽△ADE,则补充的一个条件可以是(注:只需写出一个正确答案即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】水资源透支现象令人担忧,节约用水迫在眉睫,针对居民用水浪费现象,保定市政府和环保组织进行了调查,并制定出相应的措施.
(1)据环保组织调查统计,全市至少有6×106个水龙头、2×104个抽水马桶漏水,若一万个漏水的水龙头一个月能漏掉a立方米水;一万个漏水的马桶一个月漏掉b立方米水,则全市一个月仅这两项所造成的水流失量是多少?
(2)针对居民用水浪费现象,市政府将制定居民用水标准:规定每个三口之家每月的标准用水量,超过标准部分加价收费,不超标部分的水价为每立方米3.5元;超标部分为每立方米4.2元.若某家庭某月用水12立方米,交水费44.8元,请你通过列方程求出我市规定的三口之家每月的标准用水量为多少立方米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究规律
在数轴上,把表示数1的点称为基准点,记作点O.对于两个不同点M和N,若点M和点N到点O的距离相等,则称点M与点N互为基准变换点.例如:图1中MO=NO=2,则点M和点N互为基准变换点.
发现:(1)已知点A表示数a,点B表示数b,点A与点B互为基准变换点.
①若a=0,则b= ;若a=4,则b= ;
②用含a的式子表示b,则b= ;
应用:(2)对点A进行如下操作:先把点A表示的数乘以
 ,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B.若点A与点B互为基准变换,则点A表示的数是多少?
,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B.若点A与点B互为基准变换,则点A表示的数是多少?探究:(3)点P是数轴上任意一点,对应的数为m,对P点做如下操作:P点沿数轴向右移动k(k>0)个单位长度得到P1,P2为P1的基准变换点,点P2沿数轴向右移动k个单位长度得到点P3,点P4为P3的基准变换点,“…依次顺序不断的重复,得到P6…,求出数轴上点P2018表示的数是多少?(用含m的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程:①3x﹣1=2x+1,②
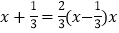 ,③
,③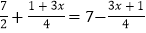 ,④
,④ x﹣1=x中,解为x=2的是方程( )
x﹣1=x中,解为x=2的是方程( )A. ①、②和③ B. ①、③和④ C. ②、③和④ D. ①、②和④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点F.请你添加一个适当的条件,使△AEF≌△CEB.添加的条件是____________(写出一个即可).
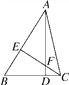
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,航空母舰始终以40千米/时的速度由西向东航行,飞机以800千米/时的速度从舰上起飞,向西航行执行任务,如果飞机在空中最多能连续飞行4个小时,那么它在起飞_____小时后就必须返航,才能安全停在舰上?

相关试题

