【题目】如图,直线y=x+m与y=nx+4n(n≠0)的交点的横坐标为2,则关于x的不等式x+m>nx+4n>0的整数解为 ( )

A. 1B. 3C. 4D. 5
参考答案:
【答案】B
【解析】
先解方程nx+4n=0得到直线y=nx+4n与x轴的交点坐标为(-4,0),然后利用函数图象写出在x轴上方且直线y=nx+4n在直线y=-x+m的下方所对应的自变量的范围,再找出此范围內的整数即可
当y=0时, nx+4n =0,解得=-4,所以直线y=nx+4n与x轴的交点坐标为(-4,0)
当x>-4时,nx+4n>0
当x<-2时,-x+m>nx+4n
所以当-4<x<-2时,-x+m>nx+4n>0
所以不等式-x+m>nx+4n>0的整数解为x=-3
故选B
-
科目: 来源: 题型:
查看答案和解析>>【题目】某出租车一天下午以车站为出发地在东西方向的大街上营运,规定向东为正,向西为负,行车里程(单位:
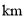 )依先后次序记录如下:
)依先后次序记录如下: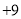 ,
, ,
,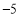 ,
,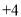 ,
,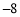 ,
,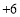 ,
, ,
,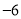 ,
,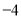 ,+10.
,+10.(1)将最后一名乘客送到目的地,出租车离车站出发点多远?在车站的什么方向?
(2)出租车在行驶过程中,离车站最远的距离是多少?
(3)出租车按物价部门规定,起步价(不超过
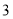 千米)为
千米)为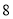 元,超过3千米的部分每千米的价格为
元,超过3千米的部分每千米的价格为 元,司机一个下午的营业额是多少?
元,司机一个下午的营业额是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场在去年底以每件80元的进价购进一批同型号的服装,一月份以每件150元的售价销售了320件,二、三月份该服装畅销,销量持续走高,在售价不变的情况下,三月底统计知三月份的销量达到了500件.
(1)求二、三月份服装销售量的平均月增长率;
(2)从四月份起商场因换季清仓采用降价促销的方式,经调查发现,在三月份销量的基础上,该服装售价每降价5元,月销售量增加10件,当每件降价多少元时,四月份可获利12000元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列说法中不正确的是( )

A. ∠1与∠AOB是同一个角B. ∠AOC也可以用∠O表示
C. ∠β=∠BOCD. 图中有三个角
-
科目: 来源: 题型:
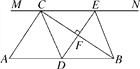
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AB=6,过点C的直线MN∥AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE.
(1)当点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由;
(2)在(1)的条件下,当∠A等于多少度时,四边形BECD是正方形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上每相邻两点间的距离为一个单位长度,点
 、
、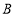 、
、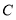 、
、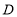 对应的数分别是
对应的数分别是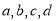 ,且
,且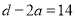 .
.(1)那么
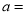 ,
,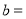 :
:(2)点
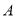 以
以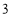 个单位/秒的速度沿着数轴的正方向运动,
个单位/秒的速度沿着数轴的正方向运动,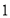 秒后点
秒后点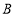 以
以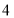 个单位/秒的速度也沿着数轴的正方向运动,当点
个单位/秒的速度也沿着数轴的正方向运动,当点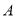 到达点
到达点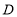 处立刻返回,与点
处立刻返回,与点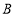 在数轴的某点处相遇,求这个点对应的数;
在数轴的某点处相遇,求这个点对应的数;(3)如果
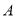 、
、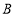 两点以(2)中的速度同时向数轴的负方向运动,点
两点以(2)中的速度同时向数轴的负方向运动,点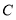 从图上的位置出发也向数轴的负方向运动,且始终保持
从图上的位置出发也向数轴的负方向运动,且始终保持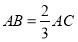 ,当点
,当点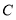 运动到
运动到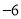 时,点
时,点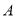 对应的数是多少?
对应的数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
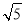 .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为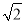 ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+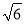 ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+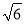 .其中正确结论的序号是( )
.其中正确结论的序号是( )
A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
相关试题

