搜索
【题目】若一个多边形的内角和为1440°，则这个多边形的边数是（ ）
A. 8B. 10C. 12D. 14
参考答案：
【答案】B
【解析】
根据多边形内角和定理：（n﹣2）×180°，列方程解答出即可．
解：根据多边形内角和定理得，（n﹣2）×180°＝1440°，解得，n＝10．
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若a是方程x2﹣5x﹣4=0的根，则a2﹣5a的值为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把Rt△ABC放在直角坐标系内，其中∠CAB＝90°，BC＝5，点A，B的坐标分别为(1，0)，(4，0)，将△ABC沿x轴向右平移，当点C落在直线y＝2x－6上时，线段BC扫过的面积为________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】请你写出一个含有字母m ， n的单项式，使它的系数为-2，次数为3．可列式为。
-
科目： 来源： 题型：
查看答案和解析>>【题目】有一组数据：2，5，7，2，3，3，6，下列结论错误的是（ ）
A. 平均数为4 B. 中位数为3 C. 众数为2 D. 极差是5
-
科目： 来源： 题型：
查看答案和解析>>【题目】[发现]如图∠ACB=∠ADB=90°，那么点D在经过A，B，C三点的圆上（如图①）
[思考]如图②，如果∠ACB=∠ADB=a（a≠90°）（点C，D在AB的同侧），那么点D还在经过A， B，C三点的圆上吗？
我们知道，如果点D不在经过A，B，C三点的圆上，那么点D要么在圆O外，要么在圆O内，以下该同学的想法说明了点D不在圆O外。
请结合图④证明点D也不在⊙O内.
[结论]综上可得结论：如图②，如果∠ACB=∠ADB=a（点C，D在AB的同侧），那么点D在经过A，B，C三点的圆上，即：点A、B、C、D四点共圆。
[应用]利用上述结论解决问题：
如图⑤，已知△ABC中，∠C=90°，将△ACB绕点A顺时针旋转一个角度得△ADE，连接BE CD，延长CD交BE于点F，
（1）求证：点B、C、A、F四点共圆；
（2）求证：BF=EF.
图⑤
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=k1x+b与反比例函数y=
的图象交于A（2，m），B（-3，﹣2）两点.（1）求m的值；
（2）根据所给条件，请直接写出不等式k1x+b＞
的解集；（3）若P（p，y1），Q（﹣2，y2）是函数y=
图象上的两点， 且y1＞y2，求实数p的取值范围.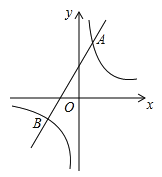
相关试题
