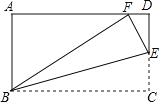
【题目】如图,在矩形![]() 中,
中,![]() ,在
,在![]() 上任取一点
上任取一点![]() ,连接
,连接![]() .将
.将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,则
处,则![]() 的面积为_______.
的面积为_______.
参考答案:
【答案】![]()
【解析】
设CE=x,由矩形的性质得出AD=BC=5,CD=AB=3,∠A=∠D=90°.由折叠的性质得出BF=BC=5,EF=CE=x,DE=CD-CE=3-x.在Rt△ABF中利用勾股定理求出AF的长度,进而求出DF的长度;然后在Rt△DEF根据勾股定理列出关于x的方程即可求出CE,再利用三角形面积求解.
解:设CE=x.
∵四边形ABCD是矩形,
∴AD=BC=5,CD=AB=3,∠A=∠D=90°.
∵将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,
∴BF=BC=5,EF=CE=x,DE=CD-CE=3-x.
在Rt△ABF中,由勾股定理得:
AF2=52-32=16,
∴AF=4,DF=5-4=1.
在Rt△DEF中,由勾股定理得:
EF2=DE2+DF2,
即x2=(3-x)2+12,
解得:x=![]() ,
,
∴DE=![]()
∴S△EDF=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
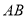 、
、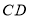 相交于
相交于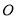 ,∠EOC=90°,
,∠EOC=90°,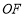 是
是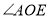 的角平分线,
的角平分线, ,求
,求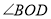 的度数.其中一种解题过程如下:请在括号中注明根据,在横线上补全步骤.
的度数.其中一种解题过程如下:请在括号中注明根据,在横线上补全步骤.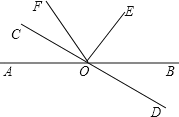
解:∵

 ( )
( )∴
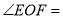
∵
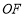 是
是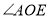 的角平分线
的角平分线∴
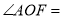
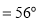 ( )
( )∴
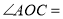
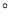
∵
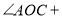
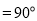
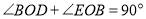 ( )
( )∴
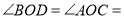
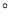 ( )
( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】下图是北京怀柔医院一位病人在4月8日6时到4月10日18时的体温记录示意图,下列说法中,错误的是
①护士每隔6小时给病人量一次体温;
②这个病人的体温最高是39.5摄氏度,最低36.8摄氏度;
③他的体温在4月9日18时到4月10日18时比较稳定;
④他的体温在4月8日18时到4月9日18时下降最快.
A. ① B. ②④ C. ④ D. ③④
-
科目: 来源: 题型:
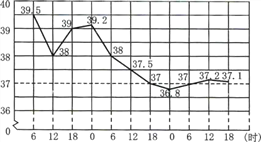
查看答案和解析>>【题目】依据国家实行的《国家学生体质健康标准》,对怀柔区初一学生身高进行抽样调查,以便总结怀柔区初一学生现存的身高问题,分析其影响因素,为学生的健康发展及学校体育教育改革提出合理项建议.已知怀柔区初一学生有男生840人,女生800人,他们的身高在150≤x<175范围内,随机抽取初一学生进行抽样调查.抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:
根据统计图表提供的信息,下列说法中
①抽取男生的样本中,身高在155≤x<165之间的学生有18人;
②初一学生中女生的身高的中位数在B组;
③抽取的样本中,抽取女生的样本容量是38;
④初一学生身高在160≤x<170之间的学生约有800人.
其中合理的是
A. ①② B. ①④ C. ②④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某个图形是按下面方法连接而成的:(0,0)→(2,0);(1,0)→(0,﹣1);(1,1)→(1,﹣2);(1,0)→(2,﹣1).
(1)请连接图案,它是一个什么汉字?
(2)作出这个图案关于y轴的轴对称图形,并写出新图案相应各端点的坐标,你得到一个什么汉字?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是“已知线段AB,求作在线段AB上方作等腰Rt△ABC.”的尺规作图的过程.
已知:线段AB.
求作:在线段AB上方作等腰Rt△ABC.
作法:如图
(1)分别以点A和点B为圆心,大于
 AB的长为半径作弧,
AB的长为半径作弧,两弧相交于E,F两点;;
(2)作直线EF,交AB于点O;
(3)以O为圆心,OA为半径作⊙O,在AB上方交EF于点C;
(4)连接线段AC,BC.
△ABC为所求的等腰Rt△ABC.
请回答:该尺规作图的依据是____________________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有一种节能型轿车的油箱加满天然气后,油箱中的剩余天然气量
 (升)与轿车行驶路程
(升)与轿车行驶路程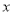 (千米)之间的关系如图所示,根据图象回答下列问题:
(千米)之间的关系如图所示,根据图象回答下列问题: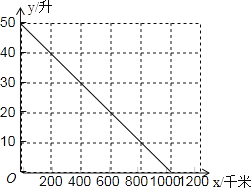
(1)这种轿车的油箱最多能装______升天然气,加满天然气后可供轿车行驶______千米.
(2)轿车每行驶200千米消耗天然气________升.
(3)写出
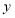 与
与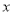 之间的函数关系式.
之间的函数关系式.
相关试题

