【题目】奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度(测角仪高度忽略不计).他们的操作方法如下:如图,他们先在B处测得最高塔塔顶A的仰角为45°,然后向最高塔的塔基直行90米到达C处,再次测得最高塔塔顶A的仰角为58°.请帮助他们计算出最高塔的高度AD约为多少米.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)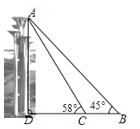
参考答案:
【答案】解:∵∠B=45°,AD⊥DB,
∴∠DAB=45°,
∴BD=AD,
设DC=x,则BD=BC+DC=90+x,
∴AD=90+x,
∴tan58°=![]() =
=![]() =1.60,
=1.60,
解得:x=150,
∴AD=90+150=240(米),
答:最高塔的高度AD约为240米.
【解析】根据已知条件求出BD=AD,设DC=x,得出AD=90+x,再根据tan58°=![]() , 求出x的值,即可得出AD的值.
, 求出x的值,即可得出AD的值.
【考点精析】本题主要考查了关于仰角俯角问题的相关知识点,需要掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.
-
科目: 来源: 题型:
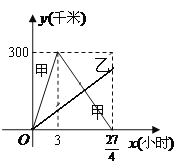
查看答案和解析>>【题目】已知:甲、乙两车分别从相距300千米的 A,B两地同时出发相向而行,其中甲到 B地后立即返回,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
(1)求甲车离出发地的距离 y(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)当它们行驶到与各自出发地的距离相等时,用了
 小时,求乙车离出发地的距离 y(千米)与行驶时间 x(小时)之间的函数关系式;
小时,求乙车离出发地的距离 y(千米)与行驶时间 x(小时)之间的函数关系式; (3)在(2)的条件下,求它们在行驶的过程中相遇的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积.
(2)在图形中作出△ABC关于x轴的对称图形△A1B1C1.写出点A1,B1,C1的坐标.
(3)在图形中作出△ABC关于y轴的对称图形△A2B2C2.写出点A2,B2,C2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线l与直线 y= -2x关于y轴对称,直线l与反比例函数
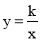 的图象的一个交点为A(2, m).
的图象的一个交点为A(2, m).(1)试确定反比例函数的表达式;
(2)若过点A的直线与x轴交于点B,且∠ABO=45°,直接写出点B的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案:
方案一:若单位赞助广告费10000元,则该单位所购门票的价格为每张60元;
(总费用=广告赞助费+门票费)
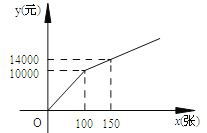
方案二:购买门票方式如图所示.
解答下列问题:
(1)方案一中,y与x的函数关系式为 ;
方案二中,当0≤x≤100时,y与x的函数关系式为 ,
当x>100时,y与x的函数关系式为 ;
(2)如果购买本场足球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由;
(3)甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张,花去总费用计58000元,求甲、乙两单位各购买门票多少张.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB是⊙O的直径.PC是⊙O的切线,C为切点,PD⊥AB于点D,交AC于点E.
(1)求证:∠PCE=∠PEC;
(2)若AB=10,ED= , sinA=
, sinA=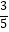 , 求PC的长.
, 求PC的长.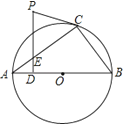
相关试题

