【题目】如图,在ABCD中,O是对角线AC和BD的交点,OE⊥AD于E,OF⊥BC于F.求证:OE=OF. 
参考答案:
【答案】证明:∵四边形ABCD是平行四边形, ∴OA=OC,AD∥BC,
∴∠EAO=∠FCO,
∵OE⊥AD,OF⊥BC,
∴∠AEO=∠CFO=90°,
在△AEO和△CFO中,
∵ 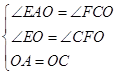 ,
,
∴△AEO≌△CFO(AAS),
∴OE=OF
【解析】由四边形ABCD是平行四边形,根据平行四边形对角线互相平分,即可得OA=OC,又由OE⊥AD,OF⊥BC,易证得△AEO≌△CFO,由全等三角形的对应边相等,可得OE=OF.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
(1)判断AB与⊙O的位置关系,并说明理由;
(2)若PF:PC=1:2,AF=5,求CP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用黑白两种颜色的正六边形地砖按如图所示的方式,拼成若干个图案:

(1)当黑色地砖有1块时,白色地砖有 块,当黑色地砖有2块时,白色地砖有 块;
(2)第n(n为正整数)个图案中,白色地砖有 块;
(3)第几个图案中有2018块白色地砖?请说明理由.
-
科目: 来源: 题型:
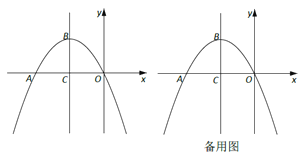
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线
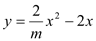 与x轴负半轴交于点A,顶点为B,且对称轴与x轴交于点C。
与x轴负半轴交于点A,顶点为B,且对称轴与x轴交于点C。(1)求点B的坐标(用含m的代数式表示);
(2)D为BD中点,直线AD交y轴于E,若点E的坐标为(0,2),求抛物线的解析式;
(3)在(2)的条件下,点M在直线BO上,且使得△AMC的周长最小,P在抛物线上,Q在直线BC上,若以A、M、P、Q为顶点的四边形是平行四边形,求点P的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若收入100元记为+100元,则-500元表示______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表为某市居民每月用水收费标准(单位:元/
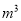 ).
).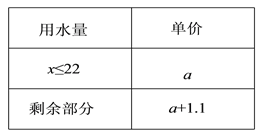
(1)某用户用水10立方米,共交水费23元,求a的值.
(2) 在(1)的前提下,该户5月份交水费71元,请问该用户用水多少立方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,随机事件是( )
A.任意画一个三角形,其内角和为180°B.经过有交通信号的路口,遇到红灯
C.在只装了红球的袋子中摸到白球D.太阳从东方升起
相关试题

