【题目】用黑白两种颜色的正六边形地砖按如图所示的方式,拼成若干个图案:

(1)当黑色地砖有1块时,白色地砖有 块,当黑色地砖有2块时,白色地砖有 块;
(2)第n(n为正整数)个图案中,白色地砖有 块;
(3)第几个图案中有2018块白色地砖?请说明理由.
参考答案:
【答案】(1)6,10;(2)4n﹢2;(3)第504个图案中有2018块白色地砖.
【解析】试题分析:观察图形,找出一般规律,由此解答即可得到结论.
试题解析:解: (1)6,10;
(2)∵每个图案都比其前一个图案多4个白色地砖,∴可得规律为:第n个图案中有白色地砖6+4(n﹣1)=(4n+2)块;
(3)令4n+2=2018,解得n=504.
答:第504个图案中有2018块白色地砖.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若单项式-x6y3m与2x2ny3是同类项,则常数m+n的值是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各式
(1)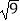 ×(
×( 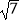 ﹣π)0+(
﹣π)0+( 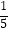 )﹣1
)﹣1
(2)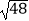 +(3﹣
+(3﹣ 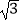 )(1+
)(1+  ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
(1)判断AB与⊙O的位置关系,并说明理由;
(2)若PF:PC=1:2,AF=5,求CP的长.

-
科目: 来源: 题型:
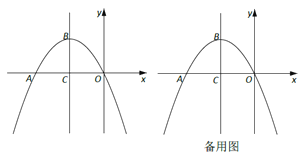
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线
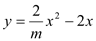 与x轴负半轴交于点A,顶点为B,且对称轴与x轴交于点C。
与x轴负半轴交于点A,顶点为B,且对称轴与x轴交于点C。(1)求点B的坐标(用含m的代数式表示);
(2)D为BD中点,直线AD交y轴于E,若点E的坐标为(0,2),求抛物线的解析式;
(3)在(2)的条件下,点M在直线BO上,且使得△AMC的周长最小,P在抛物线上,Q在直线BC上,若以A、M、P、Q为顶点的四边形是平行四边形,求点P的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,O是对角线AC和BD的交点,OE⊥AD于E,OF⊥BC于F.求证:OE=OF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若收入100元记为+100元,则-500元表示______.
相关试题

