【题目】如图,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标为O(0,0),A(2,0),B(2,2),C(4,2),D(4,4),E(0,4),若如图过点M(1,2)的直线MP(与y轴交于点P)将多边形OABCDE分割成面积相等的两部分,则直线MP的函数表达式是 . 
参考答案:
【答案】y= ![]() x+
x+ ![]()
【解析】解:延长CB交y轴于点F,
∵A(2,0),B(2,2),C(4,2),D(4,4),E(0,4),
∴S正方形OABF=OAAB=2×2=4,
S矩形CDEF=CFCD=4×2=8,
∴S多边形OABCDE=4+8=12,
设直线PG的解析式为y=kx+b(k≠0),
∵M(1,2),
∴k+b=2①,
∵点P在y轴上,
∴P(0,b),
∵C(4,2),D(4,4),
∴G(4,4k+b),
∴S梯形PGDE= ![]() (DG+PE)DE=
(DG+PE)DE= ![]() S多边形OABCDE=
S多边形OABCDE= ![]() ×(4﹣4k﹣b+4﹣b)×4=6,即8k+4b=10②,
×(4﹣4k﹣b+4﹣b)×4=6,即8k+4b=10②,
①联立得, ![]() ,
,
解得 ![]() ,
,
故此一次函数的解析式为:y= ![]() x+
x+ ![]() .
.
故答案为:y= ![]() x+
x+ ![]() .
.
延长CB交y轴于点F,根据O(0,0),A(2,0),B(2,2),C(4,2),D(4,4),E(0,4)求出多边形OABCDE的面积,设直线PG的解析式为y=kx+b(k≠0),把点M代入即可得到k+b=2,再用k、b表示出P、G两点坐标,再由S梯形PGDE= ![]() S多边形OABCDE即可得出kb的值,故可得出结论.
S多边形OABCDE即可得出kb的值,故可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=
 ∠BCD,(2)EF=CF;(3)S△BEC=2S△CEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( )
∠BCD,(2)EF=CF;(3)S△BEC=2S△CEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( ) 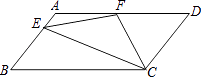
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】小红抛掷一枚质地均匀的骰子,骰子六个面分别刻有1到6的点数,下列事件为必然事件的是( )
A.骰子向上一面的点数为偶数B.骰子向上一面的点数为3
C.骰子向上一面的点数小于7D.骰子向上一面的点数为6
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A.两条射线所组成的图形叫做角
B.一条直线可以看成一个平角
C.角的两边越长,角就越大
D.角的大小和它的度数大小是一致的 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系XOY中,有A(3,2),B (﹣1,﹣4 ),P是X轴上的一点,Q是Y轴上的一点,若以点A,B,P,Q四个点为顶点的四边形是平行四边形,则Q点的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上,点
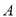 的初始位置表示的数为
的初始位置表示的数为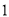 ,现点
,现点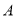 做如下移动:第
做如下移动:第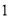 次点
次点 向左移动
向左移动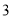 个单位长度至点
个单位长度至点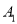 ,第
,第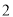 次从点
次从点 向右移动
向右移动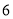 个单位长度至点
个单位长度至点 ,第
,第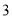 次从点
次从点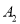 向左移动
向左移动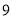 个单位长度至点
个单位长度至点 ,
,  ,按照这种移动方式进行下去,如果点
,按照这种移动方式进行下去,如果点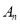 与原点的距离不小于
与原点的距离不小于 ,那么
,那么 的最小值是__________.
的最小值是__________.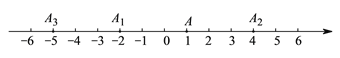
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,属于必然事件的是( )
A.2020年的除夕是晴天B.太阳从东边升起
C.打开电视正在播放新闻联播D.在一个都是白球的盒子里,摸到红球
相关试题

