【题目】如图,在ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF= ![]() ∠BCD,(2)EF=CF;(3)S△BEC=2S△CEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( )
∠BCD,(2)EF=CF;(3)S△BEC=2S△CEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( ) 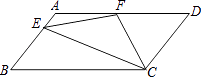
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】C
【解析】解:(1)∵F是AD的中点, ∴AF=FD,
∵在ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
∴∠DCF= ![]() ∠BCD,故正确;
∠BCD,故正确;
·(2)延长EF,交CD延长线于M,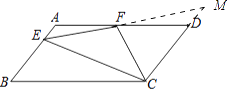
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,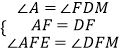 ,
,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=FM,故正确;
·(3)∵EF=FM,
∴S△EFC=S△CFM ,
∵MC>BE,
∴S△BEC<2S△EFC
故S△BEC=2S△CEF错误;
·(4)设∠FEC=x,则∠FCE=x,
∴∠DCF=∠DFC=90°﹣x,
∴∠EFC=180°﹣2x,
∴∠EFD=90°﹣x+180°﹣2x=270°﹣3x,
∵∠AEF=90°﹣x,
∴∠DFE=3∠AEF,故正确,
故选:C.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形具有而矩形不一定具有的性质是( )
A.对角线互相垂直
B.对角线相等
C.对角线互相平分
D.对角互补 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点A1 , A2 , A3 , A4和C1 , C2 , C3 , C4分别是ABCD的五等分点,点B1 , B2和D1 , D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( )
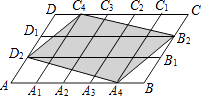
A.4
B.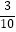
C.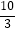
D.30 -
科目: 来源: 题型:
查看答案和解析>>【题目】两个角的和为67°56′,差是12°40′,求这两个角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红抛掷一枚质地均匀的骰子,骰子六个面分别刻有1到6的点数,下列事件为必然事件的是( )
A.骰子向上一面的点数为偶数B.骰子向上一面的点数为3
C.骰子向上一面的点数小于7D.骰子向上一面的点数为6
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A.两条射线所组成的图形叫做角
B.一条直线可以看成一个平角
C.角的两边越长,角就越大
D.角的大小和它的度数大小是一致的 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标为O(0,0),A(2,0),B(2,2),C(4,2),D(4,4),E(0,4),若如图过点M(1,2)的直线MP(与y轴交于点P)将多边形OABCDE分割成面积相等的两部分,则直线MP的函数表达式是 .

相关试题

