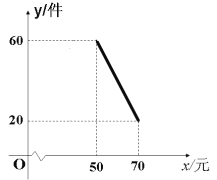
【题目】某商店试销一种新商品,该商品的进价为40元/件,经过一段时间的试销发现,每月的销售量会因售价在40~70元之间的调整而不同。当售价在40~50元时,每月销售量都为60件;当售价在50~70元时,每月销售量与售价的关系如图所示,令每月销售量为y件,售价为x元/件,每月的总利润为Q元。
(1)当售价在50~70元时,求每月销售量为y与x的函数关系式?
(2)当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
(3)若该商店每月采购这种新商品的进货款不低于1760元,则该商品每月最大利润为 元。
参考答案:
【答案】(1)y=—2x+160(50≤x≤70) ;(2)当该商品售价是60元时,该商店每月获利最大,最大利润是800元.(3)792元
【解析】试题分析:(1)由图象可知当售价在50~70元时,y与x满足一次函数的关系,可设y=kx+b(k≠0),把(50,60),,70,20)代入求出k、b的值即可;
(2)当40≤x≤50,Q=60x—2400,当50≤x≤70,Q=—2(x—60)2+800,在各自的自变量取值的范围内,由函数的增减性可求得各自的最大值,进行比较取大的一个值即可.
(3)由进货款不低于1760元,可得销售量≥44件,即—2x+160≥44,可得x≤58,再由每月利润Q=—2(x—60)2+800,可求得Q在50≤ x≤58的最大值.
试题解析:(1)令y=kx+b
由图知:当x=50时,y=60;当x=70时,y=20.
∴![]() ∴
∴![]()
∴y=—2x+160(50≤x≤70)
(2)由题可知,
当40≤x≤50
Q=60(x—40)=60x—2400
∵60>0, ∴Q随x的增大而增大,
∴x=50时,Q有最大值600元.
当50≤x≤70
Q=y(x—40)=2x2+240x—6400=—2(x—60)2+800
∵—2<0, ∴x=60时,Q有最大值800元.
综上所述,当该商品售价是60元时,该商店每月获利最大,最大利润是800元.
(3)根据题意,得40y≥1760,即y≥44,
所以-2x+160≥44,解得x≤58,
Q=-2(x-60)2+800,
因为-2<0,在对称轴x=60左侧,y随x的增大而增大,
所以当x=58时,Q有最大值,最大值为-2(58-60)2+800=792.
-
科目: 来源: 题型:
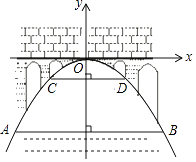
查看答案和解析>>【题目】如图,有一座抛物线型拱桥,桥下面在正常水位AB时宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升从警戒线开始,再持续多少小时才能到拱桥顶?(平面直角坐标系是以桥顶点为点O的)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中有三个点A,B,C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
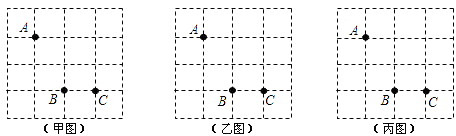
(1)在甲图中作出的四边形是中心对称图形但不是轴对称图形;
(2)在乙图中作出的四边形是轴对称图形但不是中心对称图形;
(3)在丙图中作出的四边形既是轴对称图形又是中心对称图形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在有理数中,一个数的立方等于这个数本身,这种数的个数为( )
A.1
B.2
C.3
D.无数个 -
科目: 来源: 题型:
查看答案和解析>>【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
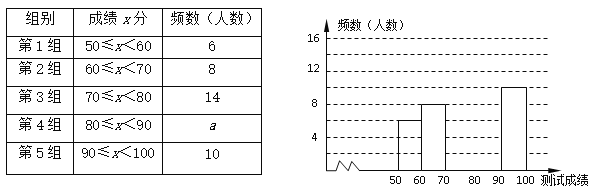
请结合图表完成下列各题:
(1)①表中a的值为 ; ②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E为矩形ABCD中AD边中点,将矩形ABCD沿CE折叠,使点D落在矩形内部的点F处,延长CF交AB于点G,连接AF.
(1)求证:AF∥CE;
(2)探究线段AF,EF,EC之间的数量关系,并说明理由;
(3)若BC=6,BG=8,求AF的长.

相关试题

