【题目】如图,点E为矩形ABCD中AD边中点,将矩形ABCD沿CE折叠,使点D落在矩形内部的点F处,延长CF交AB于点G,连接AF.
(1)求证:AF∥CE;
(2)探究线段AF,EF,EC之间的数量关系,并说明理由;
(3)若BC=6,BG=8,求AF的长.

参考答案:
【答案】(1)证明见解析;(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]()
【解析】(1)由对称的性质可得出相等的边与角,通过等腰三角形的性质及等量代换可得出∠EAF=∠DEC,即可证明AF∥CE;(2)连接DF,证△AFD、△EDC相似,根据相似的性质可推出线段AF,EF,EC之间的数量关系;(3)根据(2)中的数量关系: ![]() ,先求出EC、EF的长,进而可求出AF的长.
,先求出EC、EF的长,进而可求出AF的长.
(1)证明:由折叠矩形ABCD可得,EF=ED,CF=CD
∠DEC=∠FEC,∠EFG=∠EFC=∠EDC=90°
∵点E为AD的中点
∴AE=ED=EF
∴∠EAF=∠EFA
∵∠DEF=∠EAF+∠EFA=∠DEC+∠FEC
∴∠EAF=∠DEC
∴AF∥EC
(2)线段AF,EF,EC之间的数量关系为: ![]() ,理由如下:
,理由如下:
连接DF交EC于P
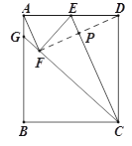
∵EF=ED, CF=CD
∴E,C两点都在线段DF的中垂线上,即EC⊥DF
∴∠DPE=90°
∵AF∥EC
∴∠AFD=∠DPE=∠EDC=90°
∵∠EAF=∠DEC,∠AFD=∠EDC
∴△AFD∽△EDC
∴![]() ,即
,即![]()
∴![]()
(3)∵∠GAF+∠EAF=∠GFA+∠EFA=90°,∠EAF=∠EFA
∴∠GAF=∠GFA,∴AG=FG
在Rt△BGC中,∵BC=6,BG=8
∴![]()
∵AB=CD=CF,∴8+AG=10-FG,∴AG=FG=1,∴CF=CD=9
∵AD=BC=6,∴![]()
∴在Rt△DEC中, ![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]()
-
科目: 来源: 题型:
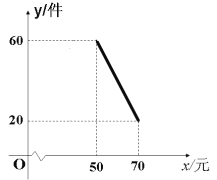
查看答案和解析>>【题目】某商店试销一种新商品,该商品的进价为40元/件,经过一段时间的试销发现,每月的销售量会因售价在40~70元之间的调整而不同。当售价在40~50元时,每月销售量都为60件;当售价在50~70元时,每月销售量与售价的关系如图所示,令每月销售量为y件,售价为x元/件,每月的总利润为Q元。
(1)当售价在50~70元时,求每月销售量为y与x的函数关系式?
(2)当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
(3)若该商店每月采购这种新商品的进货款不低于1760元,则该商品每月最大利润为 元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在有理数中,一个数的立方等于这个数本身,这种数的个数为( )
A.1
B.2
C.3
D.无数个 -
科目: 来源: 题型:
查看答案和解析>>【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
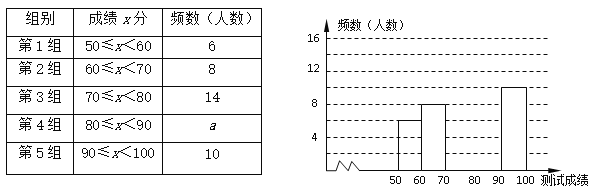
请结合图表完成下列各题:
(1)①表中a的值为 ; ②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句中表示命题的是( )
A.画一条线段B.作线段AB的垂直平分线
C.等边三角形是中心对称图形吗D.平行四边形对角线相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣(2k+1)x+4(k﹣
 )=0
)=0
(1)求证:无论k取何值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长a=4,另两边b、c恰好是这个方程的两个根,求△ABC的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两圆的半径分别为8和5,圆心距为5,那么这两圆的位置关系是( )
A.内切B.外切C.相交D.外离
相关试题

