【题目】根据下表中的二次函数 ![]() 的自变量x与函数y的对应值,可判断二次函数的图像与x轴( )
的自变量x与函数y的对应值,可判断二次函数的图像与x轴( )
A.只有一个交点
B.有两个交点,且它们分别在y轴两侧
C.有两个交点,且它们均在y轴同侧
D.无交点
参考答案:
【答案】B
【解析】根据表中的二次函数y=ax+bx+c的自变量x与函数y的对应值,可以发现当x=0,x=2时,y的值都等于 <0,
又根据二次函数的图象对称性可得:x=1是二次函数y=ax2+bx+c的对称轴,此时y有最小值2,
再根据表中的数据,可以判断出y=0时,x<1或x>2,
因此判断该二次函数的图象与x轴有两个交点,且它们分别在y轴两侧.
所以答案是:B.
【考点精析】利用二次函数的性质和二次函数的最值对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知原点为
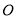 的数轴上,点
的数轴上,点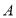 表示的数为-7,点
表示的数为-7,点 表示的数为5.
表示的数为5.
(1)若数轴上点
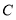 到点
到点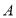 ,点
,点 的距离相等,求点
的距离相等,求点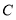 表示的数;
表示的数;(2)若数轴上点
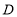 到点
到点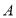 ,到点
,到点 的距离之比为
的距离之比为 ,求点
,求点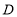 表示的数;
表示的数;(3)若一动点
 从点
从点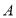 以每秒1个单位长度沿数轴向左匀速运动,同时动点
以每秒1个单位长度沿数轴向左匀速运动,同时动点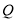 从点
从点 出发,以每秒3个单位长度沿数轴向左匀速运动,设运动的时间为
出发,以每秒3个单位长度沿数轴向左匀速运动,设运动的时间为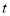 秒
秒 ,
,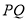 之间的距离为8个单位长度时,求
之间的距离为8个单位长度时,求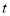 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图象如图所示,有以下结论:①
的图象如图所示,有以下结论:①  ;②
;②  ;③
;③ 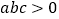 ;④
;④  ;⑤
;⑤  其中所有正确结论的序号是( )
其中所有正确结论的序号是( )
A.①②
B.①③④
C.①②③⑤
D.①②③④⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给出下列条件:①
 ;②
;②  ;③
;③  ;④
;④  其中单独能够判定
其中单独能够判定  的个数为( )
的个数为( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如下表:
原进价
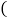 元
元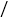 张
张
零售价
 元
元 张
张
餐桌
a
270
餐椅
b
70
若购进4张餐桌19张餐椅需要1360元;若购进6张餐桌26张餐椅需要1940元.
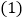 求表中a,b的值;
求表中a,b的值;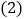 今年年初由于原材料价格上涨,每张餐桌的进价上涨了10元,每张餐椅的进价上涨了
今年年初由于原材料价格上涨,每张餐桌的进价上涨了10元,每张餐椅的进价上涨了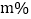 ,商场决定购进餐桌30张,餐椅170张进行销售,全部售出后,要求利润不低于7380元,求m的最大值.
,商场决定购进餐桌30张,餐椅170张进行销售,全部售出后,要求利润不低于7380元,求m的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y=
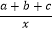 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( ) 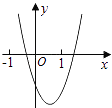
A.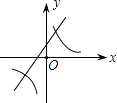
B.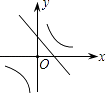
C.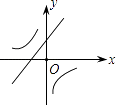
D.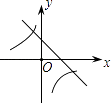
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,解决下列问题:
材料一:对非负实数x“四舍五入”到个位的值记为
 ,即:当n为非负整数时,如果
,即:当n为非负整数时,如果 ,则
,则 ;反之,当n为非负整数时,如果
;反之,当n为非负整数时,如果 ;则
;则 ,例如:
,例如: ,
, ,
, ,
,
材料二:平面直角坐标系中任意两点
 ,
, ,我们把
,我们把 叫做
叫做 、
、 两点间的折线距离,并规定
两点间的折线距离,并规定 若
若 是一定点,
是一定点, 是直线
是直线 上的一动点,我们把
上的一动点,我们把 的最小值叫做
的最小值叫做 到直线
到直线 的折线距离,例如:若
的折线距离,例如:若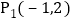 ,
, 则
则 .
. 如果
如果 ,写出实数x的取值范围;
,写出实数x的取值范围; 已知点
已知点 ,点
,点 ,且
,且 ,求a的值.
,求a的值. 若m为满足
若m为满足 的最大值,求点
的最大值,求点 到直线
到直线 的折线距离.
的折线距离.
相关试题

