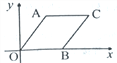
【题目】如图,在平面直角坐标系中,四边形AOBC是菱形.若点A的坐标是(3,4),则点C的坐标是____.
参考答案:
【答案】(8,4)
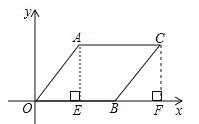
【解析】分析:过A、C作AE⊥x轴,CF⊥x轴,根据菱形的性质可得AO=AC=BO=BC=5,再证明△AOE≌△CBF,可得EO=BF,然后可得C点坐标.
详解:过A、C作AE⊥x轴,CF⊥x轴.
∵点A的坐标是(3,4),∴AO=5.
∵四边形AOBC是菱形,∴AO=AC=BO=BC=5,AO∥BC,∴∠AOB=∠CBF.
∵AE⊥x轴,CF⊥x轴,∴∠AEO=∠CFO=90°.
在△AOE和△CBF中,∵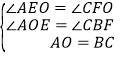 ,∴△AOE≌△CBF(AAS),∴EO=BF=3.
,∴△AOE≌△CBF(AAS),∴EO=BF=3.
∵BO=5,∴FO=8,∴C(8,4).
故答案为:(8,4).
-
科目: 来源: 题型:
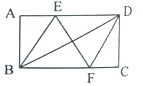
查看答案和解析>>【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为 ( )
A.
 B. 2
B. 2 C. 3
C. 3 D. 6
D. 6
-
科目: 来源: 题型:
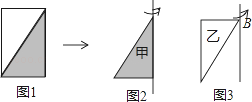
查看答案和解析>>【题目】如图1,把一张长10厘米、宽6厘米的长方形纸板分成两个相同的直角三角形.
(1)甲三角形(如图2)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方米?
(2)乙三角形(如图3)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)解方程:x2﹣2x=1;
(2)解不等式组: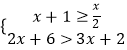 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若中学生体质健康综合评定成绩为x分,满分为100分.规定:85≤x≤100为A级,75≤x<85为B级,60≤x<75为C级,x<60为D级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图.

请根据图中的信息,解答下列问题:
(1)在这次调查中,一共抽取了名学生;a=%;C级对应的圆心角为度.
(2)补全条形统计图;
(3)若该校共有2000名学生,请你估计该校D级学生有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?

(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
-
科目: 来源: 题型:
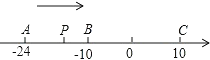
查看答案和解析>>【题目】已知数轴上有A,B,C三个点,分别表示有理数﹣24,﹣10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)用含t的代数式表示P到点A和点C的距离:
PA=________,PC=________;
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在点Q开始运动后,P,Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由.
相关试题

