搜索
【题目】如图，一枚运载火箭从地面O处发射，当火箭到达A点时，从地面C处的雷达站测得AC的距离是6km，仰角是43°，1s后，火箭到达B点，此时测得仰角为45.5°，这枚火箭从点A到点B的平均速度是多少？（结果精确到0.01）
参考答案：
【答案】火箭从A点到B点的平均速度约为0.28km/s
【解析】试题分析：首先分析图形：根据题意构造直角三角形两个直角三角形△BOC、△AOC，应利用其公共边OC构造等量关系，借助AB=OB-OA构造方程关系式，进而可求出答案．
试题解析：在Rt△OCA中，OA=ACtan43°≈4.092，
OC=ACcos43°
在Rt△OCA中，OB=OCtan45.5°≈4.375，
v=（OB﹣OA）÷t=（4.375﹣4.092）÷1≈0.28（km/s）
答：火箭从A点到B点的平均速度约为0.28km/s
-
科目： 来源： 题型：
查看答案和解析>>【题目】将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′ ，如图①所示，∠BAB′ ＝θ，
，我们将这种变换记为[θ，n] ．（1）如图①，对△ABC作变换[60°，
]得到△AB′C′ ，则
:
= ；直线BC与直线B′C′所夹的锐角为 度； （2）如图②，△ABC中，∠BAC=30°，∠ACB=90°，对△ABC作变换[θ，n]得到△AB′C′，使点B、C、
在同一直线上，且四边形ABB′C′为矩形，求θ和n的值；（3）如图③，△ABC中，AB=AC，∠BAC=36°，BC=1，对△ABC作变换[θ，n]得到△AB′C′，使点B、C、B′在同一直线上，且四边形ABB′C′为平行四边形，求θ和n的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，△ABC是等边三角形，AE=CD，BQ⊥AD于Q，BE交AD于点P，
求证：BP=2PQ．
-
科目： 来源： 题型：
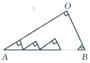
查看答案和解析>>【题目】如图所示，直角三角形ABO的周长为100，在其内部有n个小直角三角形周长之和为（ ）
A.90
B.100
C.110
D.120 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图,如果把图中任一条线段沿方格线平移1格称为“1步”,那么要通过平移使图中的3条线段首尾相接组成一个三角形,最少需要
A.4步
B.5步
C.6步
D.7步 -
科目： 来源： 题型：
查看答案和解析>>【题目】(x+3)2=x2+6x+9从左到右的变形是_________________.
-
科目： 来源： 题型：
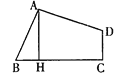
查看答案和解析>>【题目】如图所示，在四边形ABCD中，AB＝AD，∠BAD＝∠BCD＝90°，AH⊥BC于H，AH＝CH＝5，则四边形ABCD的面积是（ ）
A.15
B.20
C.25
D.无法确定
相关试题
