【题目】解答题。
(1)计算:(﹣1)2015+( ![]() )﹣3﹣(π﹣3.1)0
)﹣3﹣(π﹣3.1)0
(2)计算:(﹣2x2y)23xy÷(﹣6x2y)
(3)先化简,再求值:[(2x+y)2+(2x+y)(y﹣2x)﹣6y]÷2y,其中x=-![]() ,y=3.
,y=3.
(4)用整式乘法公式计算: ![]() .
.
参考答案:
【答案】(1)25;(2)﹣2x3y2(3),2x+y﹣3﹣1(4)620.
【解析】(1)直接利用有理数的乘方运算法则以及负整数指数幂的性质以及零指数幂的性质分别化简求出答案;
(2)直接利用积的乘方运算法则结合整式乘除运算法则化简,求出答案;
(3)首先利用乘法公式化简进而将已知数据代入求出答案;
(4)直接利用平方差公式将原式变形进而求出答案.
(1)(-1)2015+(![]() )-3-(π-3.1)0
)-3-(π-3.1)0
=-1+![]() -1
-1
=-1+27-1
=25;
(2)(-2x2y)23xy÷(-6x2y)
=4x4y23xy÷(-6x2y)
=12x5y3÷(-6x2y)
=-2x3y2;
(3)[(2x+y)2+(2x+y)(y-2x)-6y]÷2y,
=(4x2+4xy+y2+y2-4x2-6y)÷2y
=(4xy+2y2-6y)÷2y
=2x+y-3
把x=-![]() ,y=3代入得:
,y=3代入得:
原式=2×(-![]() )+3-3=-1;
)+3-3=-1;
(4)![]()
=![]()
=![]()
=620.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)解方程组

(2)x取那些整数值时,不等式
 与
与  都成立?
都成立? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,E,F是对角线BD上的点,∠1=∠2.
求证:(1)BE=DF;(2)AF∥CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】小东根据学习函数的经验,对函数y=
 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y= 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)表格是y与x的几组对应值.x
…
﹣2
﹣1
﹣

0

1

2

3
4
…
y
…



2

4

2


m
…
表中m的值为;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数y= 的大致图象;
的大致图象;
(4)结合函数图象,请写出函数y= 的一条性质: .
的一条性质: .
(5)如果方程 =a有2个解,那么a的取值范围是 .
=a有2个解,那么a的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)问题发现
如图1,△ABC和△ADE均为等边三角形,点D在边BC上,连接CE.请填空:
①∠ACE的度数为;
②线段AC、CD、CE之间的数量关系为 .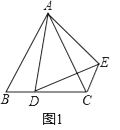
(2)拓展探究
如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在边BC上,连接CE.请判断∠ACE的度数及线段AC、CD、CE之间的数量关系,并说明理由.
(3)解决问题
如图3,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD=2,CD=1,AC与BD交于点E,请直接写出线段AC的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某体育用品专卖店销售7个篮球和9个排球的总利润为355元,销售10个篮球和20个排球的总利润为650元.
(1)求每个篮球和每个排球的销售利润;
(2)已知每个篮球的进价为200元,每个排球的进价为160元,若该专卖店计划用不超过17400元购进篮球和排球共100个,且要求篮球数量不少于排球数量的一半,请你为专卖店设计符合要求的进货方案.
相关试题

