【题目】我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)
参考答案:
【答案】解:∵∠PQB=90°﹣41°=49°,
∠BPQ=90°﹣24.5°=65.5°,
∴∠PBQ=180°﹣49°﹣65.5°=65.5°,
∴∠BPQ=∠PBQ,
∴BQ=PQ;
∵∠AQB=180°﹣49°﹣41°=90°,∠PQA=90°﹣49°=41°,
∴AQ= ![]() =
= ![]() =1600,
=1600,
∵BQ=PQ=1200,
∴AB2=AQ2+BQ2=16002+12002 ,
∴AB=2000,
答:A、B的距离为2000m.
【解析】首先由已知求出∠PBQ和∠BPQ的度数得出线段BQ与PQ,根据已知求出∠PQA,再由直角三角形PQA求出AQ,又由已知得∠AQB=90°,所以根据勾股定理求出A,B间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:四条边都相等且四个角都是直角的四边形叫做正方形。我校“快乐走班”数学兴趣小组开展了一次课外活动,过程如下:如图①,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.

(1)求证:DP=DQ;
(2)如图②,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;
(3)如图③,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)解方程组

(2)x取那些整数值时,不等式
 与
与  都成立?
都成立? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,E,F是对角线BD上的点,∠1=∠2.
求证:(1)BE=DF;(2)AF∥CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题。
(1)计算:(﹣1)2015+(
 )﹣3﹣(π﹣3.1)0
)﹣3﹣(π﹣3.1)0(2)计算:(﹣2x2y)23xy÷(﹣6x2y)
(3)先化简,再求值:[(2x+y)2+(2x+y)(y﹣2x)﹣6y]÷2y,其中x=-
 ,y=3.
,y=3. (4)用整式乘法公式计算:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】小东根据学习函数的经验,对函数y=
 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y= 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)表格是y与x的几组对应值.x
…
﹣2
﹣1
﹣

0

1

2

3
4
…
y
…



2

4

2


m
…
表中m的值为;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数y= 的大致图象;
的大致图象;
(4)结合函数图象,请写出函数y= 的一条性质: .
的一条性质: .
(5)如果方程 =a有2个解,那么a的取值范围是 .
=a有2个解,那么a的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)问题发现
如图1,△ABC和△ADE均为等边三角形,点D在边BC上,连接CE.请填空:
①∠ACE的度数为;
②线段AC、CD、CE之间的数量关系为 .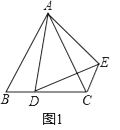
(2)拓展探究
如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在边BC上,连接CE.请判断∠ACE的度数及线段AC、CD、CE之间的数量关系,并说明理由.
(3)解决问题
如图3,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD=2,CD=1,AC与BD交于点E,请直接写出线段AC的长度.
相关试题

