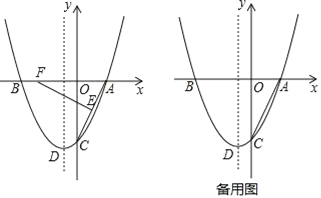
【题目】如图,抛物线y=ax2+bx﹣4与x轴交于点A(2,0)和点B,与y轴交于点C,顶点为点D,对称轴为直线x=﹣1,点E为线段AC的中点,点F为x轴上一动点.
(1)直接写出点B的坐标,并求出抛物线的函数关系式;
(2)当点F的横坐标为﹣3时,线段EF上存在点H,使△CDH的周长最小,请求出点H,使△CDH的周长最小,请求出点H的坐标;
(3)在y轴左侧的抛物线上是否存在点P,使以P,F,C,D为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)B(﹣4,0),y=![]() x2+x﹣4;(2)H(
x2+x﹣4;(2)H(![]() ,
, ![]() );(3)存在,点P的坐标为(﹣1﹣2
);(3)存在,点P的坐标为(﹣1﹣2![]() ,﹣
,﹣![]() ),(﹣1﹣
),(﹣1﹣![]() ,
, ![]() ).
).
【解析】试题分析:(1)根据轴对称,可得B点坐标,根据待定系数法,可得答案;
(2)根据自变量与函数值的对应关系,可得C点坐标,根据配方法,可得D点坐标,根据勾股定理,可得CF的长,根据等腰三角形的性质,可得A,C关于EF对称,根据轴对称的性质,可得PA=PC,根据两点之间线段最短,可得P是AD与EF的交点,根据解方程组,可得答案;
(3)根据平行四边形的对角线互相平分,可得P点的纵坐标,根据自变量与函数值的对应关系,可得答案.
解:(1)由A、B关于x=﹣1对称,得
B(﹣4,0),
∵抛物线y=ax2+bx﹣4过A(2,0)、B(﹣4,0),
∴![]() ,
,
解得: 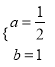 ,
,
∴y=![]() x2+x﹣4,
x2+x﹣4,
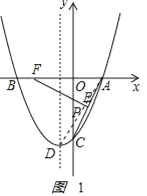
(2)如图1
 ,
,
当x=0时,y=﹣4,即C(0,﹣4),
y=![]() x2+x﹣4=
x2+x﹣4=![]() (x+1)2﹣
(x+1)2﹣![]()
∴D(﹣1,﹣ ![]() ),
),
∵E为线段AC的中点,A(2,0),C(0,﹣4),
∴E(1,﹣2).
∵点F横坐标为﹣3,
∴F(﹣3,0),
∴AF=5,CF=![]() =
=![]() =5,
=5,
∴AF=CF,
∵E为线段AC的中点,
∴EF垂直平分AC,
∴A、C关于直线EF轴对称,连接AD,与直线EF交点即为所求H,
∴EF⊥AC.
设直线EF关系式为y=k1x+b1,
∴![]() ,
,
解得: 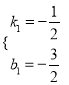 ,
,
∴直线EF:y=﹣![]() x﹣
x﹣![]() ,
,
设直线AD关系式为y=k2x+b2,
∴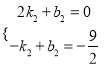 ,
,
解得: 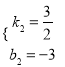 ,
,
∴y=![]() x﹣3,
x﹣3,
联立AD,EF,得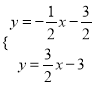 ,
,
∴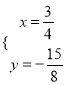 ,
,
∴H(![]() ,
, ![]() ).
).
(3)若CD为对角线,不存在;
若CD为边,则PF∥CD且PF=CD,
∵C(0,﹣4),D(﹣1,﹣ ![]() ),点F为x轴上一动点,
),点F为x轴上一动点,
如图2
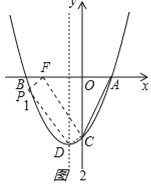 ,
,
PDCF是平行四边形,对角线的纵坐标为﹣![]() ,P点纵坐标﹣
,P点纵坐标﹣![]() ,
,
当y=﹣![]() 时,
时, ![]() x2+x﹣4=﹣
x2+x﹣4=﹣![]() ,解得x1=﹣1+2
,解得x1=﹣1+2![]() (舍),x2=﹣1﹣2
(舍),x2=﹣1﹣2![]() ,
,
∴P1(﹣1﹣2![]() ,﹣
,﹣![]() ).
).
如图3
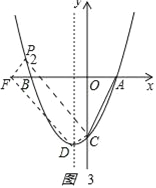 ,
,
PFDC是平行四边形,对角线的交点坐标为﹣2,P点坐标为![]() ,
,
当y=![]() 时,
时, ![]() x2+x﹣4=
x2+x﹣4=![]() ,解得x1=﹣1+
,解得x1=﹣1+![]() (舍),x2=﹣1﹣
(舍),x2=﹣1﹣![]() ,
,
∴P2(﹣1﹣![]() ,
, ![]() ).
).
综上所述:在y轴左侧的抛物线上存在点P,使以P,F,C,D为顶点的四边形是平行四边形,点P的坐标(﹣1﹣2![]() ,﹣
,﹣![]() ),(﹣1﹣
),(﹣1﹣![]() ,
, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式x2+mx+9是完全平方式,那么m=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学对八年级女生仰卧起坐的测试成绩进行统计分析,将数据整理后,画出频数分布直方图(如图).已知图中从左到右的第一、第二、第三、第四、第六小组的百分比依次是10%,15%,20%,30%,5%,第五小组的频数是36,根据所给的图填空:
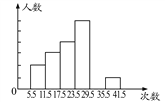
(1)第五小组的百分比是________;
(2)参加这次测试的女生人数是________;若次数在24次(含24次)以上为达标,则该校八年级女生的达标率为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
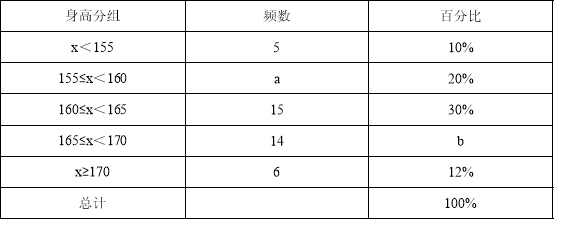
(1)填空:a= ,b= ;
(2)补全频数分布直方图;
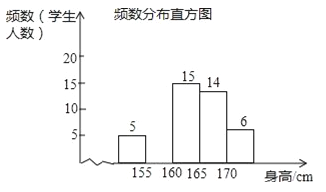
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】统计显示,2013年底某市各类高中在校学生人数约是11.4万人,将11.4万用科学记数法表示应为( )
A.11.4×104
B.1.14×104
C.1.14×105
D.0.114×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D为直线BC上一动点(点D不与B、C重合)以AD为边作正方形ADEF,使∠DAF=∠BAC,连接CF.
(1)如图1,当点D在线段BC上时,求证:BD=CF;
(2)如图2,当点D在线段BC的延长线上,且∠BAC=90°时.
①问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
②延长BA交CF于点G,连接GE,若AB=2
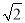 ,CD=BC,请求出GE的长.
,CD=BC,请求出GE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)一个解的范围是( )
x
3.23
3.24
3.25
3.26
ax2+bx+c
-0.06
-0.02
0.03
0.09
A. 3<x<3.23 B. 3.23<x<3.24
C. 3.24<x<3.25 D. 3.25<x<3.26
相关试题

