【题目】已知直线l1:y=(k﹣1)x+k+1和直线l2:y=kx+k+2,其中k为不小于2的自然数.
(1)当k=2时,直线l1、l2与x轴围成的三角形的面积S2=______;
(2)当k=2、3、4,……,2018时,设直线l1、l2与x轴围成的三角形的面积分别为S2,S3,S4,……,S2018,则S2+S3+S4+……+S2018=______.
参考答案:
【答案】 1 ![]()
【解析】利用一次函数图象上点的坐标特征可求出两直线与x轴的交点坐标,进而可得出两点间的距离,联立两直线解析式成方程组,通过解方程组可求出两直线的交点坐标.
(1)代入k=2,可得出d的值,利用三角形的面积公式可求出S2的值;
(2)分别代入k=2、3、4、…、2018求出S2、S3、S4、…、S2018值,将其相加即可得出结论.
当y=0时,有(k-1)x+k+1=0,
解得:x=-1-![]() ,
,
∴直线l1与x轴的交点坐标为(-1-![]() ,0),
,0),
同理,可得出:直线l2与x轴的交点坐标为(-1-![]() ,0),
,0),
∴两直线与x轴交点间的距离d=-1-![]() -(-1-
-(-1-![]() )=
)=![]() -
-![]() .
.
联立直线l1、l2成方程组,得:
![]() ,解得:
,解得:![]() ,
,
∴直线l1、l2的交点坐标为(-1,-2).
(1)当k=2时,d=![]() -
-![]() =1,
=1,
∴S2=![]() ×|-2|d=1.
×|-2|d=1.
故答案为:1.
(2)当k=3时,S3= ![]() ;当k=4时,S4=
;当k=4时,S4=![]() ;…;S2018=
;…;S2018=![]() ,
,
∴S2+S3+S4+……+S2018=![]() ,
,
=![]() ,
,
=2-![]() ,
,
=![]() .
.
故答案为:![]() ./p>
./p>
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义符号min{a,b}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如:min{2,﹣4}=﹣4,min{1,5}=1,则min{﹣x2+1,﹣x}的最大值是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6个型号)
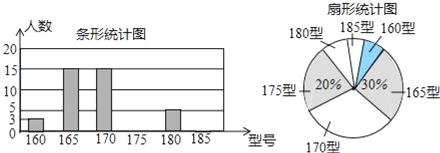
根据以上信息,解答下列问题:
(1)该班共有 名学生;
(2)在扇形统计图中,185型校服所对应的扇形圆心角的大小为 ;
(3)该班学生所穿校服型号的众数为 ,中位数为 ;
(4)如果该校预计招收新生600名,根据样本数据,估计新生穿170型校服的学生大约有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一列数
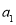 ,a2,a3,…,
,a2,a3,…,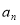 ,其中a1=-1,
,其中a1=-1,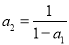 ,
,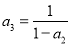 ,…,
,…,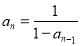 ,完成下列填空:
,完成下列填空:(1)a2 = ,a3 = ,a2019 = ;
(2)a1+a2+a3+……+a2019 = .(直接写出计算结果)
-
科目: 来源: 题型:
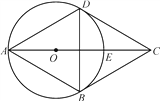
查看答案和解析>>【题目】已知:如图,四边形ABCD为菱形,△ABD的外接圆⊙O与CD相切于点D,交AC于点E.
(1)判断⊙O与BC的位置关系,并说明理由;
(2)若CE=2,求⊙O的半径r.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)(3a2﹣8a)+(2a3﹣13a2+2a)﹣2(a3﹣3),其中a=﹣2;
(2)
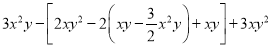 ,其中x=﹣
,其中x=﹣ ,y=3.
,y=3. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).

(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈
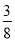 ,cos22°≈
,cos22°≈ ,tan22°≈
,tan22°≈ )
)
相关试题

