搜索
【题目】如图，E、F分别是正方形ABCD中BC和CD边上的点，CE=
BC，F为CD的中点，连接AF、AE、EF，
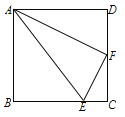
（1）判定△AEF的形状，并说明理由；
（2）设AE的中点为O,判定∠BOF和∠BAF的数量关系，并证明你的结论.
参考答案：
【答案】（1）、直角三角形，理由见解析；（2）、∠BOF=2∠BAF，证明过程见解析.
【解析】
试题分析：（1）、设正方形的边长为4a，求出
、
、
得出直角三角形；（2）、根据等腰三角形的性质和直角三角形斜边上的中线得出结论.
试题解析：（1）、设正方形的边长为4a,则
∴
∴△AEF是直角三角形
（2）、数量关系：∠BOF=2∠BAF
∵OB=OA=OF,
∴∠BOE=2∠BAE, ∠EOF=2∠EAF
∴∠BOF=2∠BAF
-
科目： 来源： 题型：
查看答案和解析>>【题目】在实数﹣3，0，5，3中，最小的实数是（ ）
A．﹣3 B．0 C．5 D．3
-
科目： 来源： 题型：
查看答案和解析>>【题目】若一个多边形的外角和等于360°，则这个多边形的边数为（ ）
A. 三 B. 四 C. 五 D. 不能确定
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，△ACD沿AD折叠，使得点C落在斜边AB上的点E处．
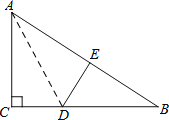
（1）求证：△BDE∽△BAC；
（2）已知AC=6，BC=8，求线段AD的长度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示，给出下列结论：①2a+b＞0；②b＞a＞c；③若-1＜m＜n＜1，则m+n＜
；④3|a|+|c|＜2|b|．其中正确的结论个数是（ ）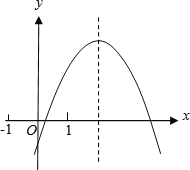
A．4 B．3 C．2 D．1
-
科目： 来源： 题型：
查看答案和解析>>【题目】小刚在课外书中看到这样一道有理数的混合运算题：
计算：
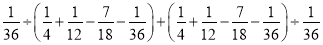
她发现，这个算式反映的是前后两部分的和，而这两部分之间存在着某种关系，利用这种关系，他顺利地解答了这道题。
（1）前后两部分之间存在着什么关系？
（2）先计算哪步分比较简便？并请计算比较简便的那部分。
（3）利用（1）中的关系，直接写出另一部分的结果。
（4）根据以上分析，求出原式的结果。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，马路边安装的路灯由支柱上端的钢管ABCD支撑，AB=25cm，CG⊥AF，FD⊥AF，点G、点F分别是垂足，BG=40cm，GF=7cm，∠ABC=120°，∠BCD=160°，请计算钢管ABCD的长度．（钢管的直径忽略不计，结果精确到1cm．参考数据：sin10°≈0.17，cos10°≈0.98，tan10°≈0.18，sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）
相关试题
