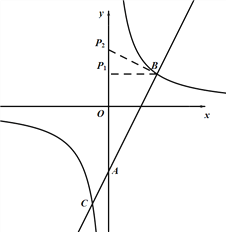
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与y轴相交于点A,与反比例函数y2=![]() (c≠0)的图象相交于点B(3,2)、C(﹣1,n).
(c≠0)的图象相交于点B(3,2)、C(﹣1,n).
(1)求一次函数和反比例函数的解析式;
(2)根据图象,直接写出y1>y2时x的取值范围;
(3)在y轴上是否存在点P,使△PAB为直角三角形?如果存在,请求点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)反比例函数解析式为: ![]() ,一次函数解析式为y1=2x﹣4;(2)由图可知,当写出y1>y2时x的取值范围是﹣1<x<0或者x>3;(3)y轴上存在点P,使△PAB为直角三角形,P1(0,2)、P2(0,
,一次函数解析式为y1=2x﹣4;(2)由图可知,当写出y1>y2时x的取值范围是﹣1<x<0或者x>3;(3)y轴上存在点P,使△PAB为直角三角形,P1(0,2)、P2(0, ![]() ).
).
【解析】试题分析:(1) 把B(3,2)代入![]() 求得k的值,即可得反比例函数解析式,把C(-1,n)代入反比例函数的解析式,求得n值,再利用待定系数法求一次函数的解析式即可;(2)观察图象,直接写出结论即可;(3)
求得k的值,即可得反比例函数解析式,把C(-1,n)代入反比例函数的解析式,求得n值,再利用待定系数法求一次函数的解析式即可;(2)观察图象,直接写出结论即可;(3)![]() 轴上存在点P,使△PAB为直角三角形,分∠B PA=90°和∠P BA=90°两种情况求点P的坐标即可.
轴上存在点P,使△PAB为直角三角形,分∠B PA=90°和∠P BA=90°两种情况求点P的坐标即可.
试题解析:
(1)把B(3,2)代入![]() 得:
得: ![]() =6
=6
∴反比例函数解析式为: ![]()
把C(-1,n)代入![]() ,得:n=-6
,得:n=-6
∴C(-1,-6)
把B(3,2)、C(-1,-6)分别代入![]() ,得:
,得:
![]() ,解得:
,解得: ![]()
所以一次函数解析式为![]()
(2)由图可知,当写出![]() >
>![]() 时
时![]() 的取值范围是-1<
的取值范围是-1<![]() <0或者
<0或者![]() >3
>3
(3)![]() 轴上存在点P,使△PAB为直角三角形
轴上存在点P,使△PAB为直角三角形
过B作BP1⊥![]() 轴于P1
轴于P1
∠B P1 A=90°,△P1AB为直角三角形
此时,P1(0,2)
过B作BP2⊥AB交![]() 轴于P2
轴于P2
∠P2 BA=90°,△P2 AB为直角三角形
在Rt△P1AB中,
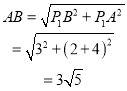
在Rt△P1 AB和Rt△P2 AB
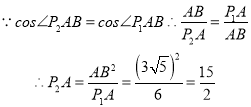
∴![]()
∴P2(0, ![]() )
)
综上所述,P1(0,2)、P2(0, ![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班为了从甲、乙两位同学中选出班长,进行了一次演讲答辩与民主测评A、B、C、D、E五位老师作为评委,对“演讲答辩”情况进行评价,全班50位同学参与了民主测评。结果如下表所示:


规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;
民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;
综合得分=演讲答辩得分×(1-a)+民主测评得分×a(0.5≤a≤0.8);
(1) 当a=0.6时,甲的综合得分是多少?
(2) 如果以综合得分来确定班长,试问:甲、乙两位同学哪一位当选为班长?并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:mx2﹣my2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】过十五边形的一个顶点可以作条对角线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区为更好的提高业主垃圾分类的意识,管理处决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买3个温馨提示牌和4个垃圾箱共需580元,且每个温馨提示牌比垃圾箱便宜40元.
(1)问购买1个温馨提示牌和1个垃圾箱各需多少元?
(2)如果需要购买温馨提示牌和垃圾箱共100个,费用不超过8000元,问最多购买垃圾箱多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市号召居民节约用水,为了解居民用水情况,随机抽查了20户家庭某月的用水量,结果如表,则这20户家庭这个月的平均用水量是吨.
用水量(吨)
4
5
6
8
户数
3
8
4
5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=EB,求∠A的度数.

相关试题

