【题目】已知一次函数y1=ax+c和反比例函数y2= ![]() 的图象如图所示,则二次函数y3=ax2+bx+c的大致图象是( )
的图象如图所示,则二次函数y3=ax2+bx+c的大致图象是( )
A.
B.
C.
D.
参考答案:
【答案】B
【解析】解:∵一次函数y1=ax+c图象过第一、二、四象限,
∴a<0,c>0,
∴二次函数y3=ax2+bx+c开口向下,与y轴交点在x轴上方;
∵反比例函数y2= ![]() 的图象在第二、四象限,
的图象在第二、四象限,
∴b<0,
∴﹣ ![]() <0,
<0,
∴二次函数y3=ax2+bx+c对称轴在y轴左侧.
满足上述条件的函数图象只有B选项.
故选B.
【考点精析】认真审题,首先需要了解一次函数的图象和性质(一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远),还要掌握反比例函数的图象(反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.

(1)求证:ACAD=ABAE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣
 x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为  m.
m. 
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论不正确的是( )
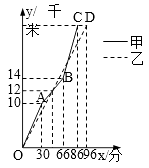
A.甲先到达终点
B.前30分钟,甲在乙的前面
C.第48分钟时,两人第一次相遇
D.这次比赛的全程是28千米 -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级(1)班班主任对本班学生进行了“我最喜欢的课外活动”的调查,并将调查结果分为书法和绘画类(记为A)、音乐类(记为B)、球类(记为C)、其他类(记为D).根据调查结果发现该班每个学生都进行了登记且只登记了一种自己最喜欢的课外活动.班主任根据调查情况把学生都进行了归类,并制作了如下两幅统计图,请你结合图中所给信息解答下列问题:
(1)七年级(1)班学生总人数为人,扇形统计图中D类所对应扇形的圆心角为度,请补全条形统计图;
(2)学校将举行书法和绘画比赛,每班需派两名学生参加,A类4名学生中有两名学生擅长书法,另两名擅长绘画.班主任现从A类4名学生中随机抽取两名学生参加比赛,请你用列表或画树状图的方法求出抽到的两名学生恰好是一名擅长书法,另一名擅长绘画的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得C的仰角为45°,已知OA=200米,山坡坡度为
 (即tan∠PAB=
(即tan∠PAB=  ),且O,A,B在同一条直线上,求电视塔OC的高度以及此人所在的位置点P的垂直高度.(侧倾器的高度忽略不计,结果保留根号)
),且O,A,B在同一条直线上,求电视塔OC的高度以及此人所在的位置点P的垂直高度.(侧倾器的高度忽略不计,结果保留根号)
相关试题

