【题目】学习几何的一个重要方法就是要学会抓住基本图形,让我们来做一次研究性学习.

(1)如图①所示的图形,像我们常见的学习用品一圆规,我们常把这样的图形叫做“规形图”.请你观察“规形图”,试探究∠BOC与∠A、∠B、∠C之间的关系,并说明理由:
(2)如图②,若△ABC中,BO平分∠ABC,CO平分∠ACB,且它们相交于点O,试探究∠BOC与∠A的关系;
(3)如图③,若△ABC中,∠ABO=![]() ∠ABC,∠ACO=
∠ABC,∠ACO=![]() ∠ACB,且BO、CO相交于点O,请直接写出∠BOC与∠A的关系式为 _.
∠ACB,且BO、CO相交于点O,请直接写出∠BOC与∠A的关系式为 _.
参考答案:
【答案】(1)∠BOC=∠BAC+∠B+∠C.理由见解析;
(2)∠BOC=90°+![]() ∠A.理由见解析;
∠A.理由见解析;
(3)∠BOC=60°+![]() ∠A.理由见解析.
∠A.理由见解析.
【解析】
(1)如图1,连接AO,延长AO到H.由三角形的外角的性质证明即可得到结论:∠BOC=∠BAC+∠B+∠C;
(2)利用角平分线的定义,三角形的内角和定理证明可得到结论:∠BOC=90°+![]() ∠A;
∠A;
(3)类似(2)可证明结论:∠BOC=60°+![]() ∠A.
∠A.
解:(1)∠BOC=∠BAC+∠B+∠C.
理由:
如图1,连接AO,延长AO到H.
∵∠BOH=∠B+∠BAH,∠CAH=∠C+∠CAH,
∴∠BOC=∠B+∠BAH+∠CAH+∠C=∠BAC+∠B+∠C,
∴∠BOC=∠BAC+∠B+∠C;
(2)∠BOC=90°+![]() ∠A.
∠A.
理由:
如图2,
∵OB,OC是△ABC的角平分线,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠BOC=180°-![]() (∠ABC+∠ACB)=180°-(180°-∠A)=90°+
(∠ABC+∠ACB)=180°-(180°-∠A)=90°+![]() ∠A,
∠A,
∴∠BOC=90°+![]() ∠A;
∠A;
(3)∠BOC=60°+![]() ∠A.
∠A.
理由:
∵∠ABO=![]() ∠ABC,∠ACO=
∠ABC,∠ACO=![]() ∠ACB,
∠ACB,
∴∠BOC=180°-![]() (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°-![]() (180°-∠A=60°+
(180°-∠A=60°+![]() ∠A.
∠A.
故答案为:∠BOC=60°+![]() ∠A.
∠A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有足够多的长方形和正方形卡片,如下图:

(1)如果选取1号、2号、3号卡片分别为l张、1张、2张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形(所画图形大小和原图保持一致),并用等式表示拼图前后面积之间的关系:
(2)小明用类似方法解释分解因式a2+5ab+4b2,请画图说明小明的方法(所画图形大小和原图保持一致),并写出分解因式的结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。
(1)求购买一个足球、一个篮球各需多少元?
(2)根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程2x2﹣5x﹣3=0. x2﹣2x=x﹣2.
(1)2x2﹣5x﹣3=0.
(2)x2﹣2x=x﹣2. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:对于任何数a,符号[a]表示不大于a的最大整数.例如:[5.7]=5,[5]=5,[-1.5]=-2.
(1)[-π]= ;
(2)如果[a]=2,那么a的取值范围是 ;
(3)如果[
 ]=-5,求满足条件的所有整数x;
]=-5,求满足条件的所有整数x;(4)直接写出方程6x-3[x]+7=0的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).

(1)将△ABC绕点B顺时针旋转90°得到△A′BC′,请画出△A′BC′.
(2)求BA边旋转到BA′位置时所扫过图形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】对任意有理数x,用[x]表示不大于x的最大整数.例如:[1.3]=1,[3]=3,[﹣2.5]=﹣3.以下结论正确的是_____.(把你认为正确结论的序号都填上)
①[﹣3.14]=﹣4;
②﹣[﹣x]=[x];
③[2x]=2[x];
④若[
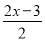 ]=﹣4,则x的取值范围是﹣
]=﹣4,则x的取值范围是﹣ ≤x<﹣
≤x<﹣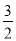 .
.
相关试题

