【题目】解决问题时需要思考:是否解决过与其类似的问题.小明从问题1解题思路中获得启发从而解决了问题2.
问题1:如图①,在正方形ABCD中,E、F是BC、CD上两点,∠EAF=45°.
求证:∠AEF=∠AEB.
小明给出的思路为:延长EB到H,满足BH=DF,连接AH.请完善小明的证明过程.

问题2:如图②,在等腰直角△ABC中,∠ACB=90°,AC=BC=4,D为AB中点,E、F是AC、BC边上两点,∠EDF=45°.
(1)求点D到EF的距离.
(2)若AE=a,则S△DEF= (用含字母a的代数式表示).
参考答案:
【答案】(1)证明见解析;(2)2,(3)a+![]() -4
-4
【解析】试题分析:问题1:如图①中,延长EB到H,满足BH=DF,连接AH,只要证明△AHE≌△AFE,即可推出∠AEF=∠AEB;
问题2:(1)如图②中,过点D分别向AC、BC、EF作垂线,垂足分别为G、H、M,利用(1)中即可,根据角平分线的性质定理即可解决问题,
(2)在Rt△DEG中,DE=![]() ,由S△AED=
,由S△AED=![]() AEDG=a,△DEF∽△AED,推出
AEDG=a,△DEF∽△AED,推出![]() ,由此即可解决问题;
,由此即可解决问题;
试题解析:问题1:证明:如图①中,延长EB到H,满足BH=DF,连接AH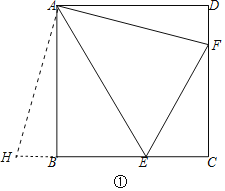
∵AB=AD,∠ABH=∠D=90°,BH=DF,
∴△ADF≌ABH,
∴∠DAF=∠BAH,AF=AH,
∵∠DAF+∠BAE=∠BAD-∠EAF=90°-45°=45°,
即∠EAH=∠BAH+∠BAE=45°,
∴∠EAH=∠EAF,
又∵AF=AH,AE=AE,
∴△AHE≌△AFE,
∴∠AEF=∠AEB.
问题2:解:(1)过点D分别向AC、BC、EF作垂线,垂足分别为G、H、M,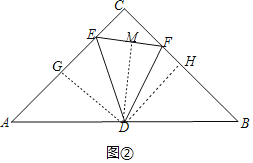
∵∠ACB=90°,∴CGDH为矩形,∵AC=BC=4,D为AB中点,
∴DG=DH=![]() BC=2,
BC=2,
∴四边形CGDH为正方形,
由问题1知∠DEG=∠DEM,
∴DM=DG=2.
(2)在Rt△DEG中,DE=![]() ,
,
∵S△AED=![]() AEDG=a,
AEDG=a,
∵△DEF∽△AED,
∴![]() ,
,
∴S△DEF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a﹣3|+(b+4)2=0,则(a+b)2018的值是( )
A. 2018B. 1C. ﹣2018D. ﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解
如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分;…;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,∠BAC是△ABC的好角.
小丽展示了确定∠BAC是△ABC的好角的两种情形.情形一:如图2,沿等腰三角形ABC顶角∠BAC的平分线AB1折叠,点B与点C重合;情形二:如图3,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,此时点B1与点C重合.
探究发现
(1)△ABC中,∠B=2∠C,经过两次折叠,∠BAC是不是△ABC的好角?(填“是”或“不是”).
(2)小丽经过三次折叠发现了∠BAC是△ABC的好角,请探究∠B与∠C(不妨设∠B>∠C)之间的等量关系.根据以上内容猜想:若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 .
应用提升
(3)小丽找到一个三角形,三个角分别为15°、60°、105°,发现60°和105°的两个角都是此三角形的好角.
请你完成,如果一个三角形的最小角是4°,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中∠C=90°,D,E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )
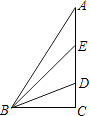
A.BC是△ABE的高
B.BE是△ABD的中线
C.BD是△EBC的角平分线
D.∠ABE=∠EBD=∠DBC -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人周末从同一地点出发去某景点,因乙临时有事,甲坐地铁先出发,甲出发0.2小时后乙开汽车前往.设甲行驶的时间为x(h),甲、乙两人行驶的路程分别为y1(km)与y2(km).如图①是y1与y2关于x的函数图像.
(1)分别求线段OA与线段BC所表示的y1与y2关于x的函数表达式;
(2)当x为多少时,两人相距6 km?
(3)设两人相距S千米,在图②所给的直角坐标系中画出S关于x的函数图像.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一件夹克衫先按成本价提高50%标价,再将标价打8折出售,结果获利28元,如果设这件夹克衫的成本价是x元,那么根据题意,所列方程正确的是( )
A.0.8(1+0.5)x=x+28
B.0.8(1+0.5)x=x﹣28
C.0.8(1+0.5x)=x﹣28
D.0.8(1+0.5x)=x+28 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:180°﹣20°40′= .
相关试题

