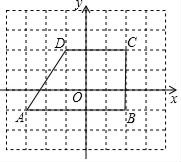
【题目】在直角坐标平面里,梯形ABCD各顶点的位置如图所示,图中每个小正方形方格的边长为1个单位长度.
(1)求梯形ABCD的面积;
(2)如果把梯形ABCD在坐标平面里先向右平移1个单位,然后向下平移2个单位得到梯形A1B1C1D1,求新顶点A1,B1,C1,D1的坐标.
参考答案:
【答案】(1)12 (2)A1(﹣2,﹣3),B1(3,﹣3),C1(3,0),D1(0,0)
【解析】试题分析:(1)判断出A、B、C、D四点坐标,利用梯形的面积公式计算即可;
(2)则平移公式为:![]() ,即可解决问题;
,即可解决问题;
试题解析:
(1)由图可知:
A(﹣3,﹣1)、B(2,﹣1)、C(2,2)、D(﹣1,2)
AB∥CD,BC⊥AB,
所以,梯形ABCD是直角梯形,
AB=5,DC=3,BC=3,
梯形ABCD的面积是S=![]()
(2)如果把梯形ABCD在坐标平面里先向右平移1个单位,然后向下平移2个单位,则平移公式为:![]()
所以,平移以后所得梯形A1B1C1D1各顶点的坐标分别为:
A1(﹣2,﹣3),B1(3,﹣3),C1(3,0),D1(0,0)
A1(-2,-3),B1(3,-3),C1(3,0),D1(0,0)
-
科目: 来源: 题型:
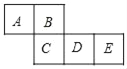
查看答案和解析>>【题目】如图是一个无盖正方体纸盒的表面展开图,请解答下列问题:
(1)若在图上补上一个同样大小的正方形F,便它能围成一个正方体,共有 种补法;
(2)请画出两种不同的补法;
(3)设A=a3+a2b+3,B=a2b﹣3,C=a3﹣1,D=6﹣a2b,若(2)中的展开图围成正方体后.相对两个面的代数式之和都相等,分别求E、F所代表的代数式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点M、N分别在线段DA、BA的延长线上,且BD=BN=DM,连接BM、DN并延长交于点P.
求证:∠P=90°﹣
 ∠C;
∠C;
-
科目: 来源: 题型:
查看答案和解析>>【题目】按要求解一元二次方程:
(1)x(x+4)=8x+12(适当方法)
(2)3x2﹣6x+2=0(配方法) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
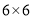 的正方形网格中,点P是
的正方形网格中,点P是 的边OB上的一点.
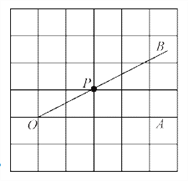
的边OB上的一点.(1)过点P画OB的垂线,交OA于点C;过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到直线__________的距离;
(3)线段__________的长度是点C到直线OB的距离;
(4)线段PC、PH、OC这三条线段大小关系是__________(用“<”号连接).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A、B两个点.
(1)如图1,若AB=a,M是AB的中点,C为线段AB上的一点,且
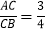 ,则AC= ,CB= ,MC= (用含a的代数式表示);
,则AC= ,CB= ,MC= (用含a的代数式表示);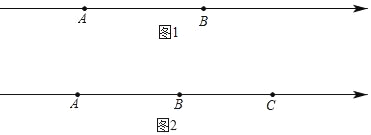
(2)如图2,若A、B、C三点对应的数分别为﹣40,﹣10,20.
①当A、C两点同时向左运动,同时B点向右运动,已知点A、B、C的速度分别为8个单位长度/秒、4个单位长度/秒、2个单位长度/秒,点M为线段AB的中点,点N为线段BC的中点,在B、C相遇前,在运动多少秒时恰好满足:MB=3BN.
②现有动点P、Q都从C点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到B点时,点Q才从C点出发,并以每秒3个单位长度的速度向左移动,且当点P到达A点时,点Q也停止移动(若设点P的运动时间为t).当PQ两点间的距离恰为18个单位时,求满足条件的时间t值.
-
科目: 来源: 题型:
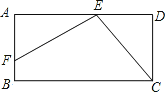
查看答案和解析>>【题目】如图,已知矩形ABCD中,E是AD上一点,F是AB上的一点,EF⊥EC,且EF=EC.
(1)求证:△AEF≌△DCE.
(2)若DE=4cm,矩形ABCD的周长为32cm,求AE的长.
相关试题

