【题目】已知数轴上有A、B两个点.
(1)如图1,若AB=a,M是AB的中点,C为线段AB上的一点,且![]() ,则AC= ,CB= ,MC= (用含a的代数式表示);
,则AC= ,CB= ,MC= (用含a的代数式表示);
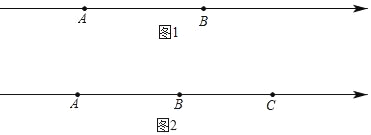
(2)如图2,若A、B、C三点对应的数分别为﹣40,﹣10,20.
①当A、C两点同时向左运动,同时B点向右运动,已知点A、B、C的速度分别为8个单位长度/秒、4个单位长度/秒、2个单位长度/秒,点M为线段AB的中点,点N为线段BC的中点,在B、C相遇前,在运动多少秒时恰好满足:MB=3BN.
②现有动点P、Q都从C点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到B点时,点Q才从C点出发,并以每秒3个单位长度的速度向左移动,且当点P到达A点时,点Q也停止移动(若设点P的运动时间为t).当PQ两点间的距离恰为18个单位时,求满足条件的时间t值.
参考答案:
【答案】(1)![]() a,
a,![]() a,
a,![]() a;(2)2秒时恰好满足MB=3BN;(3)当t为18秒、36秒和54秒时,P、Q两点相距18个单位长度.
a;(2)2秒时恰好满足MB=3BN;(3)当t为18秒、36秒和54秒时,P、Q两点相距18个单位长度.
【解析】
(1)根据题意中的等量关系用a表示出AC,CB,MC即可;
(2)①假设x秒C在B右边时,恰好满足MB=3BN,据此得出方程,求出x的值即可;
②点P表示的数为20﹣t,点Q表示的数为20﹣3(t﹣30),再分情况推论①当点P移动18秒时,②点Q在点P的右侧,③当点Q在点P的左侧,即可得出结论.
解:(1)∵AB=a,C为线段AB上的一点,且![]() =
=![]() ,
,
∴AC=![]() AB=
AB=![]() a,CB=
a,CB=![]() AB=
AB=![]() a,
a,
∵M是AB的中点,
∴MC=![]() AB﹣
AB﹣![]() AB=
AB=![]() a,
a,
故答案为:![]() a,
a,![]() a,
a,![]() a;
a;
(2)∵若A、B、C三点对应的数分别为﹣40,﹣10,20,
∴AB=BC=30,
设x秒时,C在B右边时,恰好满足MB=3BN,
∵BM=![]() (8x+4x+30),BN=
(8x+4x+30),BN=![]() (30﹣4x﹣2x),
(30﹣4x﹣2x),
∴当MB=3BN时,![]() (8x+4x+30)=3×
(8x+4x+30)=3×![]() (30﹣4x﹣2x),
(30﹣4x﹣2x),
解得:x=2,
∴2秒时恰好满足MB=3BN;
(3)点P表示的数为20﹣t,点Q表示的数为20﹣3(t﹣30),
①当点P移动18秒时,点Q没动,此时,PQ两点间的距离恰为18个单位;
②点Q在点P的右侧,∴20﹣3(t﹣30)﹣(20﹣t)=18,
解答:t=36,
③当点Q在点P的左侧,∴20﹣t﹣[20﹣3(t﹣30)]=18,
解答:t=54;
综上所述:当t为18秒、36秒和54秒时,P、Q两点相距18个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按要求解一元二次方程:
(1)x(x+4)=8x+12(适当方法)
(2)3x2﹣6x+2=0(配方法) -
科目: 来源: 题型:
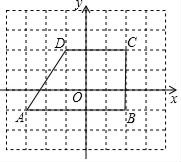
查看答案和解析>>【题目】在直角坐标平面里,梯形ABCD各顶点的位置如图所示,图中每个小正方形方格的边长为1个单位长度.
(1)求梯形ABCD的面积;
(2)如果把梯形ABCD在坐标平面里先向右平移1个单位,然后向下平移2个单位得到梯形A1B1C1D1,求新顶点A1,B1,C1,D1的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
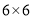 的正方形网格中,点P是
的正方形网格中,点P是 的边OB上的一点.
的边OB上的一点.(1)过点P画OB的垂线,交OA于点C;过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到直线__________的距离;
(3)线段__________的长度是点C到直线OB的距离;
(4)线段PC、PH、OC这三条线段大小关系是__________(用“<”号连接).
-
科目: 来源: 题型:
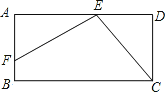
查看答案和解析>>【题目】如图,已知矩形ABCD中,E是AD上一点,F是AB上的一点,EF⊥EC,且EF=EC.
(1)求证:△AEF≌△DCE.
(2)若DE=4cm,矩形ABCD的周长为32cm,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题.
某校学生积极为地震灾区捐款奉献爱心.小颖随机抽查其中30名学生的捐款情况如下:(单位:元)2、5、35、8、5、10、15、20、15、5、45、10、2、8、20、30、40、10、15、15、30、15、8、25、25、30、15、8、10、50.
(1)这30名学生捐款的最大值、最小值、极差、平均数各是多少?
(2)将30名学生捐款额分成下面5组,请你完成频数统计表:
(3)根据上表,作出频数分布直方图.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 为了了解东北地区初中生每天体育锻炼的时间,应采用普查的方式
B. 平均数相同的甲、乙两组数据,若甲组数据的方差
 ,乙组数据的方差
,乙组数据的方差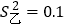 ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定C. 掷一枚质地均匀的硬币
 次,必有
次,必有 次正面朝上
次正面朝上D. 数据
 ,
, ,
, ,
, ,
,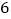 ,
, 的中位数是
的中位数是
相关试题

