搜索
【题目】如图，在正方形ABCD中，E、F分别是AB、BC上的点，且AE=BF．求证：CE=DF． 
参考答案：
【答案】证明：在正方形ABCD中，AB=BC=CD，∠B=∠BCD=90°， ∵AE=BF，
∴AB﹣AE=BC﹣BF，
即BE=CF，
在△BCE和△CDF中，
，
∴△BCE≌△CDF（SAS），
∴CE=DF．
【解析】根据正方形的性质可得AB=BC=CD，∠B=∠BCD=90°，然后求出BE=CF，再利用“边角边”证明△BCE和△CDF全等，根据全等三角形对应边相等证明即可．
【考点精析】本题主要考查了正方形的性质的相关知识点，需要掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点(1，1)，第2次接着运动到点(2，0)，第3次接着运动到点(3，2)，…，按这样的运动规律，经过第2 018次运动后，动点P的坐标是（ ）
A. (2018，0) B. (2018，1) C. (2018，2) D. (2017，0)
-
科目： 来源： 题型：
查看答案和解析>>【题目】在
中， 
、
、
三边的长分别为
、
、
，求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点
（即
三个顶点都在小正方形的顶点处），如图
所示．这样不需求
的高，而借用网格就能计算出它的面积．（1）请你将
的面积直接填写在横线上．__________________思维拓展：
（2）我们把上述求
面积的方法叫做构图法．若
三边的长分别为
、
、
（
），请利用图
的正方形网格（每个小正方形的边长为
）画出相应的
，并求出它的面积．探索创新：
（3）若
三边的长分别为
、
、
（
，且
），试运用构图法求出这三角形的面积．（请用2B铅笔将所作图形加黑加粗）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
中， 
，
；
是向右平移5个单位向上平移4个单位之后得到的图象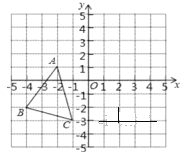
（1）
两点的坐标分别为
______________
______________.（2）作出
平移之后的图形. （3）求△ABC的面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】根据下列语句列出方程：
（1）比a小4的数是7：_____.
（2）3与x差的一半等于x的4倍______.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图1，已知
，
，可得
=______；（2）如图2，在（1）的条件下，如果
平分，则
=________；（3）如图3，在（1）（2）的条件下，如果
，则
=_________；（4）尝试解决下面问题：如图4，
，
，
是
的平分线，，求的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校为了解学生对三种国庆活动方案的意见，对该校学生进行了一次抽样调查（被调查学生至多赞成其中的一种方案），现将调查结果绘制成如图两幅不完整的统计图．
请根据图中提供的信息解答下列问题：
（1）在这次调查中共调查了名学生；扇形统计图中方案1所对应的圆心角的度数为度；
（2）请把条形统计图补充完整；
（3）已知该校有1000名学生，试估计该校赞成方案1的学生约有多少人？
相关试题
