【题目】重庆统景温泉风景区被喻为“巴渝十二景”.为丰富旅游配套资源,镇政府决定大力发动农户扩大柑橘和蔬菜种植面积,并取得了较好的经济效益.今年该镇柑橘和蔬菜的收成比去年增加了80吨,其中柑橘的收成比去年增加了20%,蔬菜的收成比去年增加了30%,从而使今年的收成共达到了420吨.
(1)统景镇去年柑橘和蔬菜的收成各是多少吨?
(2)由于今年大丰收,镇政府计划用甲、乙两种货车共33辆将柑橘和蔬菜一次性运去参加渝洽会.已知一辆甲种货车最多可装13吨柑橘和3吨蔬菜;一辆乙种货车最多可装柑橘5吨和蔬菜6吨,安排甲、乙两种货车共有几种方案?
(3)若甲种货车的运费为每辆600元,乙种货车的运费为每辆500元,在(2)的情况下,如何安排运费最少,最少为多少?
参考答案:
【答案】(1) (1)柑橘220吨,蔬菜120吨;(2)两种方案:甲车13辆,乙车20辆;甲车14辆,乙车19辆; (3)安排13辆甲车,20辆乙车。
【解析】(1)设统景镇去年柑橘和蔬菜的收成各是x,y吨,然后列出方程组求解即可;
(2)设安排甲车x辆,表示出安排乙车(33-x),然后根据运送蔬菜和水果的袋数列出不等式组求解,再根据x是正整数确定运送方案;
(3)表示出运输费用,然后根据一次函数的增减性确定运输费最少的方案即可.
解:(1)设统景镇去年柑橘和蔬菜的收成各是x,y吨,
根据题意得, ![]() ,
,
解得: ![]() ,
,
答:统景镇去年柑橘的收成是220吨,蔬菜的收成是120吨;
(2)∵220(1+20%)=264吨,120(1+30%)=156吨,
设安排甲车a辆,则安排乙车(33a),
根据题意得 ,
,
解得:12![]() a14,
a14,
∵车的辆数x是正整数,
∴x=13、14,
∴设计方案有两种:
方案一:甲车13辆,乙车20辆,
方案二:甲车14辆,乙车19辆;
(3)运输费用W=600x+500(33x)=100x+16500,
∵k=100>0,
∴W随x的增大而增大,
∴x=13时,运输费用最少,最少运输费=100×13+16500=17800元.
答:安排13辆甲车,20辆乙车运费最少,最少为17800元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是△ABC的角平分线,AE⊥CD于E,F是AC的中点,
(1)求证:EF∥BC;
(2)猜想:∠B、∠DAE、∠EAC三个角之间的关系,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市开业十周年举行了店庆活动,对A、B两种商品实行打折出售.打折前,购买5件A商品和1件B商品需用84元;购买6件A商品和3件B商品需用108元.而店庆期间,购买3件A商品和8件B商品仅需72元,求店庆期间超市的折扣是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(﹣4,4),点B的坐标为(0,1).以点A为直角顶点作∠CAD=90°,射线AC交y轴的负半轴于点C,射线AD交x轴的负半轴于点D.
(1)求直线AB的解析式;
(2)OD﹣OC的值是否为定值?如果是,求出它的值;如果不是,求出它的变化范围;
(3)平面内存在点P,使得A、B、C、P四点能构成菱形,
①P点坐标为 ;
②点Q是射线AC上的动点,求PQ+DQ的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.当容器内的水量大于5升时,求时间x的取值范围.
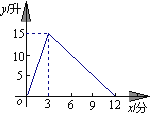
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个矩形ABCD及⊙M给出如下定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图,在平面直角坐标系xOy中,直线l:
 交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .
交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将三角形各点的横坐标都乘﹣1,纵坐标保持不变,所得图形与原图形相比有怎样的位置关系 .
相关试题

