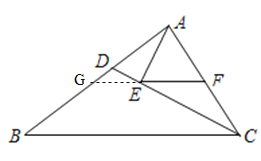
【题目】如图,CD是△ABC的角平分线,AE⊥CD于E,F是AC的中点,
(1)求证:EF∥BC;
(2)猜想:∠B、∠DAE、∠EAC三个角之间的关系,并加以证明.

参考答案:
【答案】(1)证明见解析;
(2)∠EAC=∠B+∠DAE,证明见解析.
【解析】解:(1)∵AE⊥CD于E,F是AC的中点
∴FE=FC
∴∠FEC=∠FCE
∵CD是△ABC的角平分线
∴∠ECB=∠FCE
∴∠ECB=∠FEC
∴EF∥BC .
(2)∠EAC=∠B+∠DAE.
延长FE交AD于点G;
∵EF∥BC,∴∠DGE=∠B,
∴∠DAE+∠B=∠DAE+∠G=∠AEF.
∵∠AEC=90°,F是斜边AC的中点,∴AF=EF,∴∠EAC=∠AEF.
∴∠EAC=∠B+∠DAE.
-
科目: 来源: 题型:
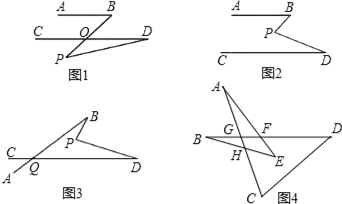
查看答案和解析>>【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D.得∠BPD=∠B﹣∠D.将点P移到AB、CD内部,如图2,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
(2)在如图2中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图3,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?(不需证明);
(3)根据(2)的结论求如图4中∠A+∠B+∠C+∠D+∠E的度数.
-
科目: 来源: 题型:
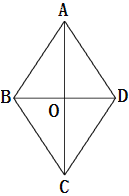
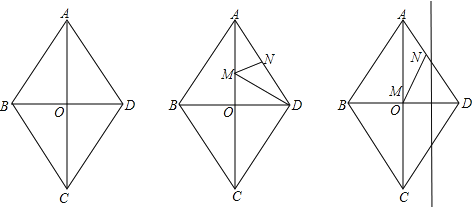
查看答案和解析>>【题目】如图,四边形ABCD是菱形,对角线AC与BD交于点O,且AC=80,BD=60.动点M、N分别以每秒1个单位的速度从点A、D同时出发,分别沿A→O→D和D→A运动,当点N到达点A时,M、N同时停止运动.设运动时间为t秒.
(1)求菱形ABCD的周长;
(2)记△DMN的面积为S,求S关于t的解析式,并求S的最大值;
(3)当t=30秒时,在线段OD的垂直平分线上是否存在点P,使得∠DPO=∠DON?若存在,这样的点P有几个?并求出点P到线段OD的距离;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由于持续高温和连日无雨,某水库的蓄水量随时间的增加而减少.已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示.针对这种干旱情况,从第10天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其它因素).
(1)求原有蓄水量y1(万m3)与干旱持续时间x(天)的函数关系式,并求x=10时的水库总蓄水量.
(2)求当0≤x≤50时,水库的总蓄水量y(万m3)与时间x(天)的函数关系式(注明x 的范围),若总蓄水量不多于840万m3为严重干旱,直接写出发生严重干旱时x的范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市开业十周年举行了店庆活动,对A、B两种商品实行打折出售.打折前,购买5件A商品和1件B商品需用84元;购买6件A商品和3件B商品需用108元.而店庆期间,购买3件A商品和8件B商品仅需72元,求店庆期间超市的折扣是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(﹣4,4),点B的坐标为(0,1).以点A为直角顶点作∠CAD=90°,射线AC交y轴的负半轴于点C,射线AD交x轴的负半轴于点D.
(1)求直线AB的解析式;
(2)OD﹣OC的值是否为定值?如果是,求出它的值;如果不是,求出它的变化范围;
(3)平面内存在点P,使得A、B、C、P四点能构成菱形,
①P点坐标为 ;
②点Q是射线AC上的动点,求PQ+DQ的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆统景温泉风景区被喻为“巴渝十二景”.为丰富旅游配套资源,镇政府决定大力发动农户扩大柑橘和蔬菜种植面积,并取得了较好的经济效益.今年该镇柑橘和蔬菜的收成比去年增加了80吨,其中柑橘的收成比去年增加了20%,蔬菜的收成比去年增加了30%,从而使今年的收成共达到了420吨.
(1)统景镇去年柑橘和蔬菜的收成各是多少吨?
(2)由于今年大丰收,镇政府计划用甲、乙两种货车共33辆将柑橘和蔬菜一次性运去参加渝洽会.已知一辆甲种货车最多可装13吨柑橘和3吨蔬菜;一辆乙种货车最多可装柑橘5吨和蔬菜6吨,安排甲、乙两种货车共有几种方案?
(3)若甲种货车的运费为每辆600元,乙种货车的运费为每辆500元,在(2)的情况下,如何安排运费最少,最少为多少?
相关试题

