【题目】如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为( ) 
A.![]()
B.![]()
C.1
D.2
参考答案:
【答案】C
【解析】解:∵OD⊥AC,AC=2,
∴AD=CD=1,
∵OD⊥AC,EF⊥AB,
∴∠ADO=∠OFE=90°,
∵OE∥AC,
∴∠DOE=∠ADO=90°,
∴∠DAO+∠DOA=90°,∠DOA+∠EF=90°,
∴∠DAO=∠EOF,
在△ADO和△OFE中, ,
,
∴△ADO≌△OFE(AAS),
∴OF=AD=1,
故选C.
【考点精析】本题主要考查了垂径定理的相关知识点,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC内接于⊙O,点D在OC的延长线上,sinB=
 ,∠CAD=30°.
,∠CAD=30°.
(1)求证:AD是⊙O的切线;
(2)若OD⊥AB,BC=5,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的东南方向上的B处.这时,海轮所在的B处距离灯塔P有多远?(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.
B.
C.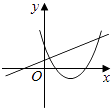
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(
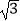 ,1)关于x轴的对称点为点A1 , 将OA绕原点O逆时针方向旋转90°到OA2 , 用扇形OA1A2围成一个圆锥,则该圆锥的底面圆的半径为 .
,1)关于x轴的对称点为点A1 , 将OA绕原点O逆时针方向旋转90°到OA2 , 用扇形OA1A2围成一个圆锥,则该圆锥的底面圆的半径为 . 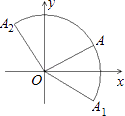
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
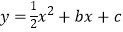 与直线
与直线 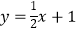 交于A、B两点,点A在x轴上,点B的横坐标是2.点P在直线AB上方的抛物线上,过点P分别作PC∥y轴、PD∥x轴,与直线AB交于点C、D,以PC、PD为边作矩形PCQD,设点Q的坐标为(m,n).
交于A、B两点,点A在x轴上,点B的横坐标是2.点P在直线AB上方的抛物线上,过点P分别作PC∥y轴、PD∥x轴,与直线AB交于点C、D,以PC、PD为边作矩形PCQD,设点Q的坐标为(m,n).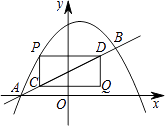
(1)点A的坐标是 , 点B的坐标是;
(2)求这条抛物线所对应的函数关系式;
(3)求m与n之间的函数关系式(不要求写出自变量n的取值范围);
(4)请直接写出矩形PCQD的周长最大时n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一批单价为20元的商品,若每件按24元的价格销售时,每天能卖出36件;若每件按29元的价格销售时,每天能卖出21件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.
(1)求y与x满足的函数关系式(不要求写出x的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润P最大?
相关试题

