【题目】如图,抛物线 ![]() 与直线
与直线 ![]() 交于A、B两点,点A在x轴上,点B的横坐标是2.点P在直线AB上方的抛物线上,过点P分别作PC∥y轴、PD∥x轴,与直线AB交于点C、D,以PC、PD为边作矩形PCQD,设点Q的坐标为(m,n).
交于A、B两点,点A在x轴上,点B的横坐标是2.点P在直线AB上方的抛物线上,过点P分别作PC∥y轴、PD∥x轴,与直线AB交于点C、D,以PC、PD为边作矩形PCQD,设点Q的坐标为(m,n).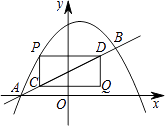
(1)点A的坐标是 , 点B的坐标是;
(2)求这条抛物线所对应的函数关系式;
(3)求m与n之间的函数关系式(不要求写出自变量n的取值范围);
(4)请直接写出矩形PCQD的周长最大时n的值.
参考答案:
【答案】
(1)(﹣2,0);(2,2)
(2)
解:由题意,得 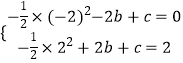 ,
,
解得 ![]()
所以,这条抛物线所对应的函数关系式为y=﹣ ![]() x2+
x2+ ![]() x+3;
x+3;
(3)
解:∵点Q的坐标为(m,n),
∴ ![]() x+1=n,
x+1=n,
解得x=2n﹣2,
所以,点C的坐标为(2n﹣2,n),
点D的坐标为(m, ![]() m+1),
m+1),
∴点P的坐标为(2n﹣2, ![]() m+1),
m+1),
将(2n﹣2, ![]() m+1)代入y=﹣
m+1)代入y=﹣ ![]() x2+
x2+ ![]() x+3,得﹣
x+3,得﹣ ![]() ×(2n﹣2)2+
×(2n﹣2)2+ ![]() ×(2n﹣2)+3=
×(2n﹣2)+3= ![]() m+1,
m+1,
整理得,m=﹣4n2+10n﹣2,
所以,m,n之间的函数关系式是m=﹣4n2+10n﹣2;
(4)
解:∵C(2n﹣2,n),P(2n﹣2, ![]() m+1),Q(m,n),
m+1),Q(m,n),
∴PC= ![]() m+1﹣n,CQ=m﹣(2n﹣2)=m﹣2n+2,
m+1﹣n,CQ=m﹣(2n﹣2)=m﹣2n+2,
∴矩形PCQD的周长=2( ![]() m+1﹣n+m﹣2n+2),
m+1﹣n+m﹣2n+2),
=3m﹣6n+6,
=3(﹣4n2+10n﹣2)﹣6n+6,
=﹣12n2+24n,
=﹣12(n﹣1)2+12,
∴当n=1时,矩形PCQD的周长最大.
【解析】解:(1)令y=0,则 ![]() x+1=0,
x+1=0,
解得x=﹣2,
所以,点A(﹣2,0),
∵点B的横坐标是2,
∴y= ![]() ×2+1=2,
×2+1=2,
∴B(2,2);
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.
B.
C.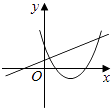
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为( )

A.
B.
C.1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(
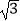 ,1)关于x轴的对称点为点A1 , 将OA绕原点O逆时针方向旋转90°到OA2 , 用扇形OA1A2围成一个圆锥,则该圆锥的底面圆的半径为 .
,1)关于x轴的对称点为点A1 , 将OA绕原点O逆时针方向旋转90°到OA2 , 用扇形OA1A2围成一个圆锥,则该圆锥的底面圆的半径为 . 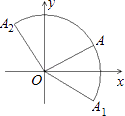
-
科目: 来源: 题型:
查看答案和解析>>【题目】一批单价为20元的商品,若每件按24元的价格销售时,每天能卖出36件;若每件按29元的价格销售时,每天能卖出21件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.
(1)求y与x满足的函数关系式(不要求写出x的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润P最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB与x轴、y轴分别交于点A和点B,OA=4,且OA,OB长是关于x的方程x2﹣mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM,交x轴于点N,点D为OA的中点.

(1)求证:CD是⊙M的切线;
(2)求线段ON的长.
相关试题

