【题目】七(1)班为“壮丽70年,奋斗新时代”演讲比赛购买A,B两种奖品.已知A奖品每件x元,B奖品每件y元.
⑴ 若购买A奖品m件,B奖品n件,共需要多少元;
⑵ 设购买A奖品m件,购买A,B两种奖品共10件:
① 购买两种奖品共需要多少元;
② 若购买A奖品至少2件,B奖品至少6件,请设计出购买方案,并说明每种方案的共需要多少元.
参考答案:
【答案】(1)![]() +
+![]() 元;
元;
(2)①![]() +
+![]() 元;
元;
②方案一:购买A奖品2件,B奖品8件;则一共需要的费用为![]() 元.
元.
方案二:购买A奖品3件,B奖品7件;则一共需要的费用为![]() 元.
元.
方案三:购买A奖品4件,B奖品6件;则一共需要的费用为![]() 元.
元.
【解析】
(1)根据费用=单价![]() 数量,总费用=两种奖品的费用之和列出关系式即可;
数量,总费用=两种奖品的费用之和列出关系式即可;
(2)①根据题意列代数式即可;
②根据题意列出不等式组,求出m的范围,即可得到所有的方案.
(1)根据题意,购买A奖品的费用为![]() 元,购买B奖品的费用为
元,购买B奖品的费用为![]() 元,
元,
则购买A,B两种奖品,一共需要的费用为![]() +
+![]() 元,
元,
答:共需要![]() +
+![]() 元;
元;
(2)①根据题意,购买A奖品的费用为![]() 元,购买B奖品的费用为
元,购买B奖品的费用为![]() 元,
元,
则购买两种奖品,一共需要的费用为![]() +
+![]() 元,
元,
答:购买两种奖品共需要![]() +
+![]() 元;
元;
②由题意知![]() ,解得
,解得![]() (m为正整数),
(m为正整数),
方案一:购买A奖品2件,B奖品8件;则一共需要的费用为![]() 元;
元;
方案二:购买A奖品3件,B奖品7件;则一共需要的费用为![]() 元;
元;
方案三:购买A奖品4件,B奖品6件;则一共需要的费用为![]() 元.
元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节吃粽子是中华民族的传统习惯.农历五月初五早晨,小王的妈妈用不透明袋子装着一些粽子(粽子除食材不同外,其他一切相同),其中糯米粽两个,还有一些薯粉粽,现小王从中任意拿出一个是糯米粽的概率为
 .
.(1)求袋子中薯粉粽的个数;
(2)小王第一次任意拿出一个粽子(不放回),第二次再拿出一个粽子,请你用树形图或列表法,求小王两次拿到的都是薯粉粽的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】10袋小麦称重后记录如下(单位:kg).88.8,91,91.5,89,91.2,91.3,88.9,91.2,91,91.1.
(1)如果每袋小麦以90 kg为标准,超过的千克数记作正数,不足的千克数记作负数,这10袋小麦总计超过多少千克或不足多少千克?
(2)10袋小麦一共多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数
 (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.(1)求△OCD的面积;
(2)当BE=
 AC时,求CE的长.
AC时,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:菱形ABCD的对角线AC,BD相交于点O,AC=
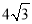 ,BD=
,BD=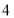 ,动点P在线段BD上从点B向点D运动,PF⊥AB于点F,PG⊥BC于点G,四边形QEDH与四边形PFBG关于点O中心对称,设菱形ABCD被这两个四边形盖住部分的面积为S1,未被盖住部分的面积为S2,
,动点P在线段BD上从点B向点D运动,PF⊥AB于点F,PG⊥BC于点G,四边形QEDH与四边形PFBG关于点O中心对称,设菱形ABCD被这两个四边形盖住部分的面积为S1,未被盖住部分的面积为S2,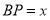 ,若S1=S2,则
,若S1=S2,则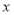 的值是( )
的值是( )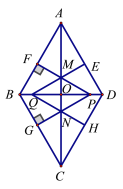
A.
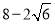 B.
B. 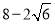 或
或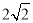 C.
C. 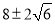 D. 不存在
D. 不存在 -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
(1)如图1,当点E在边DC上自D向C移动,同时点F在边CB上自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的数量关系和位置关系,并说明理;
(2)如图2,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不需证明);连接AC,求△ACE为等腰三角形时CE:CD的值;
(3)如图3,当E,F分别在直线DC,CB上移动时,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP的最大值.

图1 图2 图3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为某班35名学生投篮成绩的条形图,其中上面部分数据破损导致数据不完全,已知此班学生投篮成绩的中位数是5,下列选项正确的是_______.
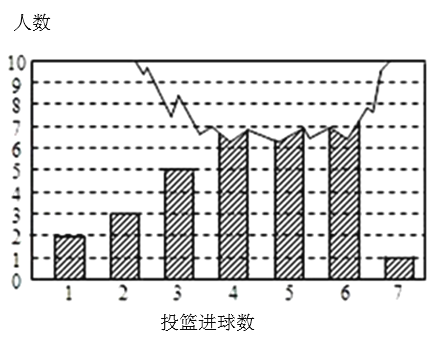
①3球以下(含3球)的人数;②4球以下(含4球)的人数; ③5球以下(含5球)的人数;④6球以下(含6球)的人数.
相关试题

