【题目】如图,已知函数![]() (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(1)求△OCD的面积;
(2)当BE=![]() AC时,求CE的长.
AC时,求CE的长.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据函数![]() (x>0)的图象经过点A(1,2),求函数解析式,再有AC∥y轴,AC=1求出C点坐标,然后根据CD∥x轴,求D点坐标,从而可求CD长,最后利用三角形面积公式求出△OCD的面积.
(x>0)的图象经过点A(1,2),求函数解析式,再有AC∥y轴,AC=1求出C点坐标,然后根据CD∥x轴,求D点坐标,从而可求CD长,最后利用三角形面积公式求出△OCD的面积.
(2)通过BE=![]() AC,求得B点坐标,进而求得CE长.
AC,求得B点坐标,进而求得CE长.
试题解析:解:(1)∵函数![]() (x>0)的图象经过点A(1,2),
(x>0)的图象经过点A(1,2),
∴![]() ,即k=2.
,即k=2.
∵AC∥y轴,AC=1,∴点C的坐标为(1,1).
∵ CD∥x轴,点D在函数图像上,∴点D的坐标为(2,1).
∴![]() .
.
(2)∵BE=![]() AC,∴BE=
AC,∴BE=![]() .
.
∵BE⊥CD,∴点B的纵坐标是![]() .∴点B的横坐标是
.∴点B的横坐标是![]() .
.
∴CE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现小明步行12 000步与小红步行9 000步消耗的能量相同.若每消耗1千卡能量小明行走的步数比小红多10步,求小红每消耗1千卡能量需要行走多少步?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了弘扬“社会主义核心价值观”,市政府在广场树立公益广告牌,如图所示,为固定广告牌,在两侧加固钢缆,已知钢缆底端D距广告牌立柱距离CD为3米,从D点测得广告牌顶端A点和底端B点的仰角分别是60°和45°.
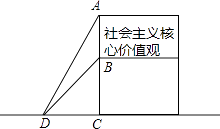
(1)求公益广告牌的高度AB;
(2)求加固钢缆AD和BD的长.(注意:本题中的计算过程和结果均保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现小明步行12 000步与小红步行9 000步消耗的能量相同.若每消耗1千卡能量小明行走的步数比小红多10步,求小红每消耗1千卡能量需要行走多少步?
【答案】小红每消耗1千卡能量需要行走30步.
【解析】分析:设小红每消耗1千卡能量需要行走x步,则小明每消耗1千卡能量需要行走(x+10)步,根据数量关系消耗能量千卡数=行走步数÷每消耗1千卡能量需要行走步数结合小明步行12000步与小红步行9000步消耗的能量相同,即可得出关于x的分式方程,解之后经检验即可得出结论.
详解:设小红每消耗1千卡能量需要行走x步,则小明每消耗1千卡能量需要行走(x+10)步,
根据题意,得 ,
,
解得x=30.
经检验:x=30是原方程的解.
答:小红每消耗1千卡能量需要行走30步.点睛:本题考查了分式方程的应用,根据数量关系消耗能量千卡数=行走步数÷每消耗1千卡能量需要行走步数列出关于x的分式方程是解题的关键.
【题型】解答题
【结束】
25【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于F,连接CF.
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF为正方形,请你添加适当的条件并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数
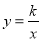 (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.(1)求△OCD的面积;
(2)当BE=
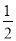 AC时,求CE的长.
AC时,求CE的长.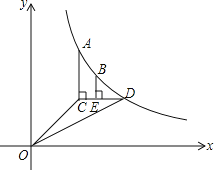
【答案】(1)
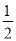 ;(2)
;(2)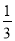 .
.【解析】试题分析:(1)根据函数
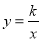 (x>0)的图象经过点A(1,2),求函数解析式,再有AC∥y轴,AC=1求出C点坐标,然后根据CD∥x轴,求D点坐标,从而可求CD长,最后利用三角形面积公式求出△OCD的面积.
(x>0)的图象经过点A(1,2),求函数解析式,再有AC∥y轴,AC=1求出C点坐标,然后根据CD∥x轴,求D点坐标,从而可求CD长,最后利用三角形面积公式求出△OCD的面积.(2)通过BE=
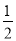 AC,求得B点坐标,进而求得CE长.
AC,求得B点坐标,进而求得CE长.试题解析:解:(1)∵函数
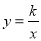 (x>0)的图象经过点A(1,2),
(x>0)的图象经过点A(1,2),∴
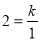 ,即k=2.
,即k=2.∵AC∥y轴,AC=1,∴点C的坐标为(1,1).
∵ CD∥x轴,点D在函数图像上,∴点D的坐标为(2,1).
∴
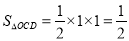 .
.(2)∵BE=
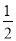 AC,∴BE=
AC,∴BE=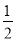 .
.∵BE⊥CD,∴点B的纵坐标是
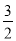 .∴点B的横坐标是
.∴点B的横坐标是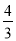 .
.∴CE=
 .
.考点:1.反比例函数综合题;3.曲线上点的坐标与方程的关系;3.三角形的面积.
【题型】解答题
【结束】
27【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:
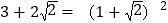 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:设
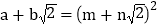 (其中
(其中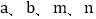 均为整数),则有
均为整数),则有 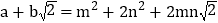 .
.∴
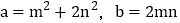 .这样小明就找到了一种把部分
.这样小明就找到了一种把部分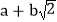 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
(1)当
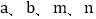 均为正整数时,若
均为正整数时,若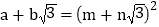 ,用含m、n的式子分别表示
,用含m、n的式子分别表示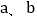 ,得
,得 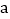 = ,
= ,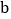 = ;
= ;(2)利用所探索的结论,找一组正整数
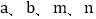 ,填空: +
,填空: + 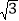 =( +
=( + 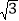 )2;
)2;(3)若
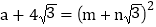 ,且
,且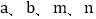 均为正整数,求
均为正整数,求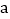 的值.
的值. -
科目: 来源: 题型:
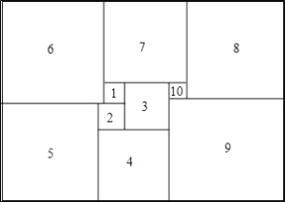
查看答案和解析>>【题目】如图所示,1925年数学家莫伦发现的世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形.若标注①、②的正方形边长分别为5和6,请你直接写出以下数据:
(1)第6个正方形的边长= ;
(2)第8个正方形的边长= ;
(3)整个长方形的面积= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年某月的月历上圈出了相邻的三个数a、b、c,并求出了它们的和为39,这三个数在月历中的排布不可能是( )
A.
 B.
B. 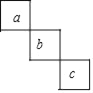 C.
C. 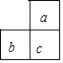 D.
D. 
相关试题

