【题目】在三角形ABC中,点D在线段AB上,DE∥BC交AC于点E,点F在直线BC上,作直线EF,过点D作直线DH∥AC交直线EF于点H.
(1)在如图1所示的情况下,求证:∠HDE=∠C;
(2)若三角形ABC不变,D,E两点的位置也不变,点F在直线BC上运动.
①当点H在三角形ABC内部时,直接写出∠DHF与∠FEC的数量关系;
②当点H在三角形ABC外部时,①中结论是否依然成立?请在图2中画图探究,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)①∠DHF+∠FEC=180°;②当点H在三角形ABC外部时,∠DHF=∠FEC,理由见解析.
【解析】
(1)根据“平行线的性质”结合“已知条件”分析证明即可;
(2)①如图1,当点H在△ABC内部时,由DH∥AC可得∠FEC=∠DHE,结合∠DHE+∠DHF=180°,即可得到:此时∠DHF+∠FEC=180°;
②当点H不在△ABC内部时,分点H在直线DE的上方和下方两种情况画出图形,如图2-1和图2-2所示,再根据“平行线的性质”结合“已知条件”进行分析证明可得:此时∠DHF=∠FEC.
(1)∵DE∥BC,
∴∠ADE=∠C,
∵DH∥AC,
∴∠HDE=∠ADE.
(2)①当点H在△ABC内部时,∠DHF+∠FEC=180°,理由如下:
∵DH∥AC,
∴∠FEC=∠DHE,
又∵∠DHE+∠DHF=180°,
∴∠DHF+∠FEC=180°;
②当点H在△ABC外部时,①中结论不成立,理由如下:
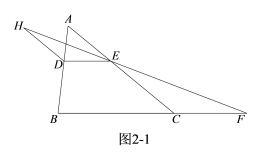
ⅰ).如图2-1,当点H在直线DE上方时,
∵DH∥AC,
∴∠DHF=∠FEC.
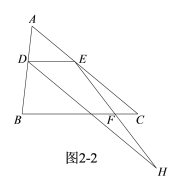
ⅱ).如图2-2,当点H在直线DE下方时,
∵DH∥AC,
∴∠DHF=∠FEC.
综上所述,当点H在△ABC外部时,∠DHF=∠FEC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )

A.5πcm2
B.10πcm2
C.15πcm2
D.20πcm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC三个顶点的坐标分别为A(0,4),B(﹣1,1),C(﹣2,2),将△ABC向右平移4个单位,得到△A′B′C′,点A,B,C的对应点分别为A′、B′、C′,再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,点A′、B′、C′的对应点分别为A″、B″、C″,则点A″的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,AD=8,P、E分别是线段AC、BC上的点,且四边形PEFD是矩形,若△PCD是等腰三角形,求AP的长.

-
科目: 来源: 题型:
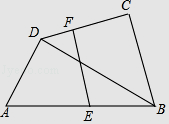
查看答案和解析>>【题目】一副三角板按如图方式摆放,得到△ABD和△BCD,其中∠ADB=∠BCD=90°,∠A=60°,∠CBD=45°,E为AB的中点,过点E作EF⊥CD于点F.若AD=4cm,则EF的长为cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:(﹣2)3+( )﹣2﹣
)﹣2﹣ 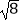 sin45°
sin45°
(2)分解因式:(y+2x)2﹣(x+2y)2 . -
科目: 来源: 题型:
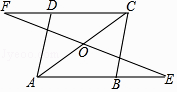
查看答案和解析>>【题目】已知:如图,在ABCD中,延长AB至点E,延长CD至点F,使得BE=DF.连接EF,与对角线AC交于点O. 求证:OE=OF.
相关试题

