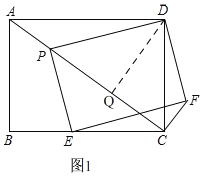
【题目】如图,矩形ABCD中,AB=6,AD=8,P、E分别是线段AC、BC上的点,且四边形PEFD是矩形,若△PCD是等腰三角形,求AP的长.

参考答案:
【答案】AP=4或AP=5或AP=![]()
【解析】试题分析:先求出AC,再分三种情况讨论计算即可得出结论.
试题解析:在矩形ABCD中,AB=6,AD=8,∠ADC=90°,
∴DC=AB=6,
∴AC=![]() =10,
=10,
要使△PCD是等腰三角形,
①当CP=CD时,AP=AC-CP=10-6=4,
②当PD=PC时,∠PDC=∠PCD,
∵∠PCD+∠PAD=∠PDC+∠PDA=90°,
∴∠PAD=∠PDA,
∴PD=PA,
∴PA=PC,
∴AP=![]() AC=5,
AC=5,
③当DP=DC时,如图1,过点D作DQ⊥AC于Q,则PQ=CQ,
∵S△ADC=![]() ADDC=
ADDC=![]() ACDQ,
ACDQ,
∴DQ=![]() ,
,
∴CQ=![]() ,
,
∴PC=2CQ=![]() ,
,
∴AP=AC-PC=10-![]() =
=![]() ;
;
所以,若△PCD是等腰三角形时,AP=4或5或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数
 ,导致了第一次数学危机,
,导致了第一次数学危机,  是无理数的证明如下: 假设
是无理数的证明如下: 假设  是有理数,那么它可以表示成
是有理数,那么它可以表示成  (p与q是互质的两个正整数).于是(
(p与q是互质的两个正整数).于是(  )2=(
)2=(  )2=2,所以,q2=2p2 . 于是q2是偶数,进而q是偶数,从而可设q=2m,所以(2m)2=2p2 , p2=2m2 , 于是可得p也是偶数.这与“p与q是互质的两个正整数”矛盾.从而可知“
)2=2,所以,q2=2p2 . 于是q2是偶数,进而q是偶数,从而可设q=2m,所以(2m)2=2p2 , p2=2m2 , 于是可得p也是偶数.这与“p与q是互质的两个正整数”矛盾.从而可知“  是有理数”的假设不成立,所以,
是有理数”的假设不成立,所以,  是无理数.
是无理数.
这种证明“ 是无理数”的方法是( )
是无理数”的方法是( )
A.综合法
B.反证法
C.举反例法
D.数学归纳法 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )

A.5πcm2
B.10πcm2
C.15πcm2
D.20πcm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC三个顶点的坐标分别为A(0,4),B(﹣1,1),C(﹣2,2),将△ABC向右平移4个单位,得到△A′B′C′,点A,B,C的对应点分别为A′、B′、C′,再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,点A′、B′、C′的对应点分别为A″、B″、C″,则点A″的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在三角形ABC中,点D在线段AB上,DE∥BC交AC于点E,点F在直线BC上,作直线EF,过点D作直线DH∥AC交直线EF于点H.
(1)在如图1所示的情况下,求证:∠HDE=∠C;
(2)若三角形ABC不变,D,E两点的位置也不变,点F在直线BC上运动.
①当点H在三角形ABC内部时,直接写出∠DHF与∠FEC的数量关系;
②当点H在三角形ABC外部时,①中结论是否依然成立?请在图2中画图探究,并说明理由.

-
科目: 来源: 题型:
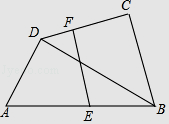
查看答案和解析>>【题目】一副三角板按如图方式摆放,得到△ABD和△BCD,其中∠ADB=∠BCD=90°,∠A=60°,∠CBD=45°,E为AB的中点,过点E作EF⊥CD于点F.若AD=4cm,则EF的长为cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:(﹣2)3+( )﹣2﹣
)﹣2﹣ 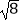 sin45°
sin45°
(2)分解因式:(y+2x)2﹣(x+2y)2 .
相关试题

