【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB’C’,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是___________ (结果保留π)

参考答案:
【答案】![]()
【解析】
根据等腰直角三角形的性质得到AC=BC=![]() ,再根据旋转的性质得到AC′=AC=
,再根据旋转的性质得到AC′=AC=![]() ,AB′=AB=2,∠BAB′=45°,∠B′AC′=45°,而S阴影部分=S扇形ABB′+S△AB′C′-S△ABC-S扇形ACC′=S扇形ABB′-S扇形ACC′,根据扇形的面积公式计算即可.
,AB′=AB=2,∠BAB′=45°,∠B′AC′=45°,而S阴影部分=S扇形ABB′+S△AB′C′-S△ABC-S扇形ACC′=S扇形ABB′-S扇形ACC′,根据扇形的面积公式计算即可.
解:∵∠ACB=90°,CB=AC,AB=2,
∴AC=BC=![]() ,
,
∵△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,
∴AC′=AC=![]() ,AB′=AB=2,∠BAB′=45°,∠B′AC′=45°,
,AB′=AB=2,∠BAB′=45°,∠B′AC′=45°,
∴S阴影部分=S扇形ABB′+S△AB′C′-S△ABC-S扇形ACC′=S扇形ABB′-S扇形ACC′
=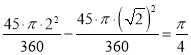 .
.
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 请阅读下列材料,并解答相应的问题:
将若干个数组成一个正方形数阵,若任意一行,一列及对角线上的数字之和都相等,则称具有这种性质的数字方阵为“幻方”中国古代称“幻方”为“河图“、“洛书“等,例如,下面是三个三阶幻方,是将数字1,2,3,4,5,6,7,8,9填入到3×3的方格中得到的,其每行、每列、每条对角线上的三个数之和相等.
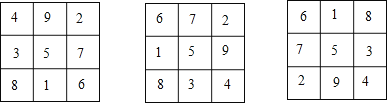
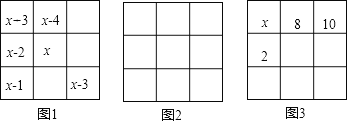
(1)设图1的三阶幻方中间的数字是x,用x的代数式表示幻方中9个数的和为 ;
(2)请你将下列九个数:﹣10、﹣8、﹣6、﹣4、﹣2、0、2、4、6分别填入图2方格中,使得每行、每列、每条对角线上的三个数之和都相等;
(3)图3是一个三阶幻方,那么标有x的方格中所填的数是 ;
(4)如图4所示的每一个圆中分别填写了1、2、3…19中的一个数字(不同的圆中填写的数字各不相同),使得图中每一个横或斜方向的线段上几个圆内的数之和都相等,现在已知该图中七个圆内的数字,则图中的x= ,y= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=
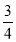 x2﹣
x2﹣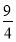 x﹣3,与x轴交于A和B两点(点A在点B的左侧),与y轴交于点C,过点A的直线与抛物线在第一象限的交点M的横坐标为
x﹣3,与x轴交于A和B两点(点A在点B的左侧),与y轴交于点C,过点A的直线与抛物线在第一象限的交点M的横坐标为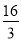 ,直线AM与y轴交于点D,连接BC、AC.
,直线AM与y轴交于点D,连接BC、AC.(1)求直线AD和BC的解折式;
(2)如图2,E为直线BC下方的抛物线上一点,当△BCE的面积最大时,一线段FG=4
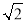 (点F在G的左侧)在直线AM上移动,顺次连接B、E、F、G四点构成四边形BEFG,请求出当四边形BEFG的周长最小时点F的坐标;
(点F在G的左侧)在直线AM上移动,顺次连接B、E、F、G四点构成四边形BEFG,请求出当四边形BEFG的周长最小时点F的坐标;(3)如图3,将△DAC绕点D逆时针旋转角度α(0°<α<180°),记旋转中的三角形为△DA′C′,若直线A′C′分别与直线BC、y轴交于M、N,当△CMN是等腰三角形时,请直接写出CM的长度.
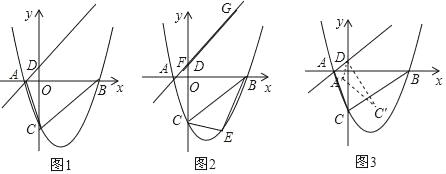
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(﹣2,0),B(0,1),以线段AB为边在第二象限作矩形ABCD,双曲线y=
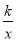 (k<0)过点D,连接BD,若四边形OADB的面积为6,则k的值是( )
(k<0)过点D,连接BD,若四边形OADB的面积为6,则k的值是( )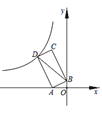
A.﹣9B.﹣12C.﹣16D.﹣18
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2-12ax+36a-5的图象在4<x<5这一段位于x轴下方,在8<x<9这一段位于x轴上方,则a的值为___________
-
科目: 来源: 题型:
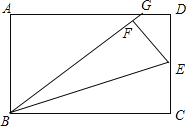
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是CD的中点,将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,将BF延长交AD于点G.若
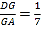 ,则
,则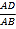 =__.
=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】春节期间某商场搞促销活动,方案是:在一个不透明的箱子里放4个完全相同的小球,球上分别标“0元”、“20元”、“30元”、“50元”,顾客每消费满300元,就可从箱子里同时摸出两个球,根据这两个小球所标金额之和可获相应价格的礼品;
(1)若某顾客在甲商商场消费320元,至少可得价值______元的礼品,至多可得价值______元的礼品;
(2)请用画树状图或列表的方法,求该顾客去商场消费,获得礼品的总价值不低于50元的概率.
相关试题

