【题目】规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是 . (写出所有正确说法的序号) ①当x=1.7时,[x]+(x)+[x)=6;
②当x=﹣2.1时,[x]+(x)+[x)=﹣7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有两个交点.
参考答案:
【答案】②③
【解析】解:①当x=1.7时, [x]+(x)+[x)
=[1.7]+(1.7)+[1.7)=1+2+2=5,故①错误;②当x=﹣2.1时,
[x]+(x)+[x)
=[﹣2.1]+(﹣2.1)+[﹣2.1)
=(﹣3)+(﹣2)+(﹣2)=﹣7,故②正确;③当1<x<1.5时,
4[x]+3(x)+[x)
=4×1+3×2+1
=4+6+1
=11,故③正确;④∵﹣1<x<1时,
∴当﹣1<x<﹣0.5时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当﹣0.5<x<0时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当x=0时,y=[x]+(x)+x=0+0+0=0,
当0<x<0.5时,y=[x]+(x)+x=0+1+x=x+1,
当0.5<x<1时,y=[x]+(x)+x=0+1+x=x+1,
∵y=4x,则x﹣1=4x时,得x= ![]() ;x+1=4x时,得x=
;x+1=4x时,得x= ![]() ;当x=0时,y=4x=0,
;当x=0时,y=4x=0,
∴当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有三个交点,故④错误,
所以答案是:②③.
【考点精析】利用一元一次不等式组的解法和有理数大小比较对题目进行判断即可得到答案,需要熟知解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 );有理数比大小:1、正数的绝对值越大,这个数越大2、正数永远比0大,负数永远比0小3、正数大于一切负数4、两个负数比大小,绝对值大的反而小5、数轴上的两个数,右边的数总比左边的数大6、大数-小数 > 0,小数-大数 < 0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正整数中,
(1﹣
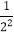 )=(1﹣
)=(1﹣ )(1+
)(1+ )
)(1﹣
 )=(1﹣
)=(1﹣ )(1+
)(1+ )
)(1﹣
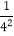 )=(1﹣
)=(1﹣ )(1+
)(1+ )
)观察上面的算式,可以归纳得出:
 = .
= .利用上述规律,计算下列各式:(1﹣
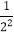 )×(1﹣
)×(1﹣ )×(1﹣
)×(1﹣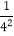 )= .
)= .(1﹣
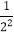 )×(1﹣
)×(1﹣ )×(1﹣
)×(1﹣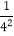 )×…×(1﹣
)×…×(1﹣ )= (请将结题步骤写在下方空白处)
)= (请将结题步骤写在下方空白处) -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料,并解答问题.
材料:将分式
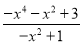 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.解:由分母为﹣x2+1,可设﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b则﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b=﹣x4﹣ax2+x2+a+b=﹣x4﹣(a﹣1)x2+(a+b)
∵对应任意x,上述等式均成立,∴
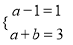 ,∴a=2,b=1
,∴a=2,b=1∴
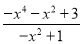 =
=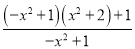 =
=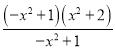 +
+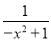 =x2+2+
=x2+2+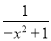 这样,分式
这样,分式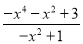 被拆分成了一个整式x2+2与一个分式
被拆分成了一个整式x2+2与一个分式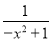 的和.
的和.解答:
(1)将分式
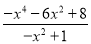 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.(2)试说明
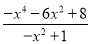 的最小值为8.
的最小值为8. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P,Q两点停止运动.
(1)AC= cm,BC= cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,P与Q第一次相遇;
(4)当t为何值时,PQ=1cm.
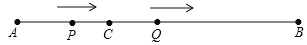
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蔬菜公司收购蔬菜260吨,准备加工后上市销售.该公司的加工能力是:每天精加工8吨或粗加工20吨.现计划在22天内完成加工任务,且尽可能多的精加工,该公司应安排几天精加工,几天粗加工,才能按期完成任务?如果每吨蔬菜粗加工后的利润是1500元,精加工后的利润为3000元,那么该公司出售这些加工后的蔬菜共可获利多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算(2017﹣π)0﹣( )﹣1+|﹣2|
)﹣1+|﹣2|
(2)化简(1﹣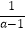 )÷(
)÷( 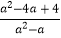 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】商场正在销售帐篷和棉被两种防寒商品,已知购买1顶帐篷和2床棉被共需300元,购买2顶帐篷和3床棉被共需510元.
(1)求1顶帐篷和1床棉被的价格各是多少元?
(2)某学校准备购买这两种防寒商品共80件,送给青海玉树灾区,要求每种商品都要购买,且帐篷的数量多于棉被的数量,但因为学校资金不足,购买总金额不能超过8500元,请问学校共有几种购买方案?(要求写出具体的购买方案.
相关试题

