搜索
【题目】在正整数中，
（1﹣
）=（1﹣
）（1+）
（1﹣
）=（1﹣
）（1+）
（1﹣
）=（1﹣
）（1+）
观察上面的算式，可以归纳得出：
= ．
利用上述规律，计算下列各式：（1﹣）×（1﹣）×（1﹣）= ．
（1﹣）×（1﹣）×（1﹣）×…×（1﹣
）= （请将结题步骤写在下方空白处）
参考答案：
【答案】（1﹣
）（1+）；
；
．
【解析】
观察一系列等式得出一般性规律，写出即可；
利用得出的规律分解因式，然后计算即可得到结果．
解：归纳得出：
=
；
计算：
×
×
=（1﹣
）（1+）（1﹣
）（1+）（1﹣
）（1+）
=×
×
×
×
×
=×
=；
（1﹣
）×（1﹣
）×（1﹣
）×…×（1﹣
）
=（1﹣）（1+）（1﹣）（1+）（1﹣）（1+）…（1+
）
=×
=
故答案为；；．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在“双十二”期间，A，B两个超市开展促销活动，活动方式如下：
A超市：购物金额打9折后，若超过2000元再优惠300元；
B超市：购物金额打8折．
某学校计划购买某品牌的篮球做奖品，该品牌的篮球在A，B两个超市的标价相同．根据商场的活动方式：
（1）若一次性付款4200元购买这种篮球，则在B商场购买的数量比在A商场购买的数量多5个．请求出这种篮球的标价；
（2）学校计划购买100个篮球，请你设计一个购买方案，使所需的费用最少．（直接写出方案）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，⊙O的内接正五边形ABCDE的对角线AD与BE相交于点G，AE=2，则EG的长是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是一个正方体的展开图，标注了字母
，
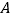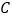的面分别是正方体的正面和底面，其他面分别用字母
，
，
，
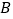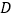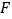表示．已知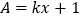
，
，
，
，
，
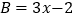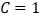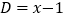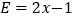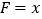．(1)如果正方体的左面与右面所标注字母代表的代数式的值相等，求出
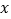的值；(2)如果正面字母
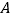代表的代数式与对面字母代表的代数式的值相等，且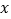为整数，求整数
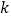的值．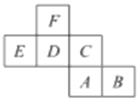
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料，并解答问题．
材料：将分式
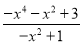拆分成一个整式与一个分式（分子为整数）的和的形式．解：由分母为﹣x2+1，可设﹣x4﹣x2+3=（﹣x2+1）（x2+a）+b则﹣x4﹣x2+3=（﹣x2+1）（x2+a）+b=﹣x4﹣ax2+x2+a+b=﹣x4﹣（a﹣1）x2+（a+b）
∵对应任意x，上述等式均成立，∴
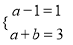，∴a=2，b=1∴
=
=
+
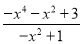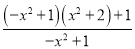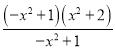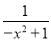=x2+2+
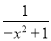这样，分式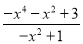
被拆分成了一个整式x2+2与一个分式
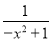的和．解答：
（1）将分式
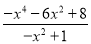拆分成一个整式与一个分式（分子为整数）的和的形式．（2）试说明
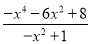的最小值为8． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB=12cm，点C是线段AB上的一点，BC=2AC．动点P从点A出发，以3cm/s的速度向右运动，到达点B后立即返回，以3cm/s的速度向左运动；动点Q从点C出发，以1cm/s的速度向右运动．设它们同时出发，运动时间为ts．当点P与点Q第二次重合时，P，Q两点停止运动．
（1）AC= cm，BC= cm；
（2）当t为何值时，AP=PQ；
（3）当t为何值时，P与Q第一次相遇；
（4）当t为何值时，PQ=1cm．
-
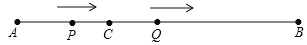
科目： 来源： 题型：
查看答案和解析>>【题目】规定：[x]表示不大于x的最大整数，（x）表示不小于x的最小整数，[x）表示最接近x的整数（x≠n+0.5，n为整数），例如：[2.3]=2，（2.3）=3，[2.3）=2．则下列说法正确的是 ． （写出所有正确说法的序号） ①当x=1.7时，[x]+（x）+[x）=6；
②当x=﹣2.1时，[x]+（x）+[x）=﹣7；
③方程4[x]+3（x）+[x）=11的解为1＜x＜1.5；
④当﹣1＜x＜1时，函数y=[x]+（x）+x的图象与正比例函数y=4x的图象有两个交点．
相关试题
