【题目】如图所示,二次函数y=ax2+bx+c(a≠0)的图象,有下列4个结论:①abc>0;②b>a+c;③4a+2b+c>0;④b2﹣4ac>0;其中正确的是 
参考答案:
【答案】③④
【解析】解:①∵抛物线的开口向下,对称轴为x=1,抛物线与y轴的交点在y轴正半轴, ∴a<0,b=﹣2a>0,c>0,
∴abc<0,结论①不符合题意;②∵当x=1时,y>0,
∴a+b+c>0,
∴b>﹣a﹣c,结论②不符合题意;③∵抛物线的对称轴为x=1,
∴当x=0与x=2时,y值相等.
∵抛物线与y轴的交点在y轴正半轴,
∴4a+2b+c=c>0,结论③符合题意;④∵抛物线与x轴有两个不相等的实数根,
∴一元二次方程ax2+bx+c=0有两个不相等的实数根,
∴△=b2﹣4ac>0,结论④符合题意.
所以答案是:③④.
【考点精析】关于本题考查的二次函数图象以及系数a、b、c的关系,需要了解二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为13,弦AB∥CD,AB=24,CD=10,则AB、CD之间的距离为( )
A.17
B.7
C.12
D.7或17 -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax2+bx与y=ax+b的图象可能是( )
A.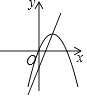
B.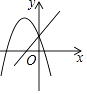
C.
D.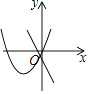
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )

A.(2,5)
B.(5,2)
C.(4, )
)
D.( ,4)
,4) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xOy中,△ABC的三个顶点坐标分别为A(﹣4,1)、B(﹣1,1)、C(﹣4,3).

(1)画出Rt△ABC关于原点O成中心对称的图形Rt△A1B1C1;
(2)若Rt△ABC与Rt△A2BC2关于点B中心对称,则点A2的坐标为、C2的坐标为
(3)求点A绕点B旋转180°到点A2时,点A在运动过程中经过的路程. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个质地均匀的小正方体,六个面分别标有数字“1”“2”“3”“4”“5”“6”.连续两次抛掷小正方体,观察每次朝上一面的数字.
(1)请用列表格或画树状图的方法列举出两次抛掷的所有可能结果;
(2)求出第二次抛掷的数字大于第一次抛掷的数字的概率;
(3)求两次抛掷的数字之和为5的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,C为
 的中点,若∠CBD=30°,⊙O的半径为12.
的中点,若∠CBD=30°,⊙O的半径为12. 
(1)求∠BAD的度数;
(2)求扇形OCD的面积.
相关试题

