Question

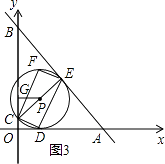
【题目】如图，在平面直角坐标系中，直线AB与x轴，y轴分别交于点A（6，0），B（0，8），点C的坐标为（0，m），过点C作CE⊥AB于点E，点D为x轴上的一动点，连接CD，DE，以CD，DE为边作CDEF．

（1）当0＜m＜8时，求CE的长（用含m的代数式表示）；
（2）当m=3时，是否存在点D，使CDEF的顶点F恰好落在y轴上？若存在，求出点D的坐标；若不存在，请说明理由；
（3）点D在整个运动过程中，若存在唯一的位置，使得CDEF为矩形，请求出所有满足条件的m的值．

Answer 1

【答案】
（1）

解：∵A（6，0），B（0，8）．

∴OA=6，OB=8．

∴AB=10，

∵∠CEB=∠AOB=90°，

又∵∠OBA=∠EBC，

∴△BCE∽△BAO，

∴ = ，即 = ，

∴CE= ﹣ m

（2）

解：∵m=3，

∴BC=8﹣m=5，CE= ﹣ m=3．

∴BE=4，

∴AE=AB﹣BE=6．

∵点F落在y轴上（如图2）．

∴DE∥BO，

∴△EDA∽△BOA，

∴ = 即 = ．

∴OD= ，

∴点D的坐标为（ ，0）

（3）

解：取CE的中点P，过P作PG⊥y轴于点G．

则CP= CE= ﹣ m．

（Ⅰ）当m＞0时，

①当0＜m＜8时，如图3．易证∠GCP=∠BAO，

∴cos∠GCP=cos∠BAO= ，

∴CG=CPcos∠GCP= （ ﹣ m）= ﹣ m．

∴OG=OC+CG=m+ ﹣ m= m+ ．

根据题意得，得：OG=CP，

∴ m+ = ﹣ m，

解得：m= ；

②当m≥8时，OG＞CP，显然不存在满足条件的m的值．

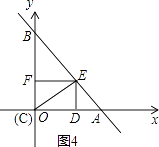
（Ⅱ）当m=0时，即点C与原点O重合（如图4）．

（Ⅲ）当m＜0时，

①当点E与点A重合时，（如图5），

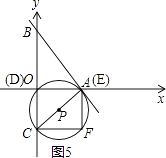
易证△COA∽△AOB，

∴ = ，即 = ，

解得：m=﹣ ．

②当点E与点A不重合时，（如图6）．

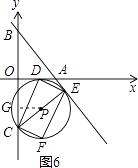
OG=OC﹣CG=﹣m﹣（ ﹣ m）

=﹣ m﹣ ．

由题意得：OG=CP，

∴﹣ m﹣ = ﹣ m．

解得m=﹣ ．

综上所述，m的值是 或0或﹣ 或﹣ ．

【解析】（1）首先证明△BCE∽△BAO，根据相似三角形的对应边的比相等即可求得；（2）证明△EDA∽△BOA，根据相似三角形的对应边的比相等即可求得；（3）分m＞0，m=0和m＜0三种情况进行讨论，当m=0时，一定成立，当m＞0时，分0＜m＜8和m＞8两种情况，利用三角函数的定义即可求解．当m＜0时，分点E与点A重合和点E与点A不重合时，两种情况进行讨论．