【题目】(本题10分) 如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.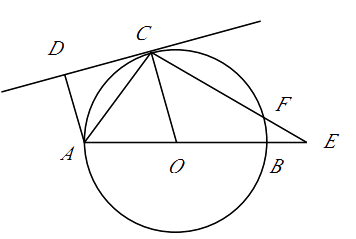
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数.
②若⊙O的半径为2 ![]() ,求线段EF的长.
,求线段EF的长.
参考答案:
【答案】
(1)
解:∵直线与⊙O相切,
∴OC⊥CD;
又∵AD⊥CD,
∴AD//OC,
∴∠DAC=∠OCA;
又∵OC=OA,
∴∠OAC=∠OCA,
∴∠DAC=∠OAC;
∴AC平分∠DAO.
(2)
解:①∵AD//OC,∠DAO=105°,
∴∠EOC=∠DAO=105°;
∵∠E=30°,
∴∠OCE=45°.
②作OG⊥CE于点G,可得FG=CG,
∵OC=2![]() ,∠OCE=45°.
,∠OCE=45°.
∴CG=OG=2,
∴FG=2;
∵在RT△OGE中,∠E=30°,
∴GE=2![]() ,
,
∴EF=GE-FG=2![]() -2.
-2.
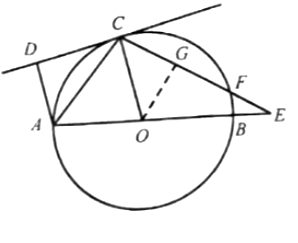
【解析】(1)利用了切线的性质,平行线的判定和性质,等边对等角,角平分线的判定即可得证。
(2)①根据(1)得出的AD//OC,从而得出同位角相等,再利用三角形的内角和定理即可求出答案;②作OG⊥CE于点G,可得FG=CG,根据等边对等角得出CG=OG=FG=2,在根据勾股定理得出GE,从而求出EF=GE-FG.
【考点精析】认真审题,首先需要了解平行线的判定与性质(由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质),还要掌握三角形的内角和外角(三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角)的相关知识才是答题的关键.
-
科目: 来源: 题型:
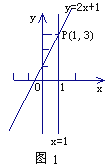
查看答案和解析>>【题目】阅读,我们知道,在数轴上,x=1表示一个点,而在平面坐标系中,x=1表示一条直线;我们还知道,以二元一次方程2x-y+1=0的所有解为坐标的点组成的图形,就是一次函数y=2x+1的图象,它也是一条直线,如图1,可以得出,直线x=1与直线y=2x+1的交点P的坐标(1,3)就是方程组
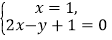 的解,所以这个方程组的解为
的解,所以这个方程组的解为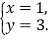
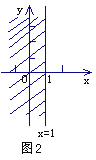
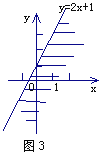
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它的左侧的部分,如图2;y≤2x+1,也表示一个平面区域,即直线y=2x+1以及它下方的部分,如图3.
回答下列问题:
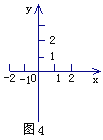
(1)在直角坐标系(如图4)中,用作图的方法求方程组
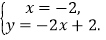 的解;
的解;(2)用阴影表示
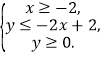 所围成的区域.
所围成的区域. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分) 如图1,将△ABC纸片沿中位线EH折叠,使点A的对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形.类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩 形,这样的矩形称为叠合矩形.




(1)将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段 , ;S矩形AEFG:S□ABCD=
(2)ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5,EH=12,求AD的长.
(3)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10.小明把该纸片折叠,得到叠合正方形.请你帮助画出叠合正方形的示意图,并求出AD,BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
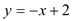 与
与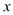 轴、
轴、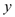 轴交点分别为
轴交点分别为 、
、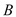 ,另一直线
,另一直线
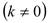 经过
经过 ,且把
,且把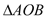 分成两部分.
分成两部分.(1)若
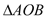 被分成的两部分面积相等,求
被分成的两部分面积相等,求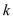 和
和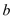 的值.
的值.(2)若
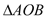 被分成的两部分面积之比为
被分成的两部分面积之比为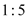 ,求
,求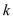 和
和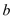 的值.
的值.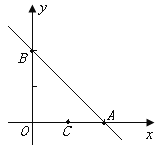
-
科目: 来源: 题型:
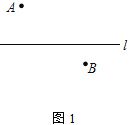
查看答案和解析>>【题目】(1) 如图1,在一条笔直的公路两侧,分别有A、B两个村庄,现在要在公路l旁建一座火力发电厂,向A、B两个村庄供电,为使所用的电线最短,请问供电厂P应健在何处?画出图形,不写作法,保留作图痕迹;
(2) 如图2,若要向4个村庄A、B、C、D供电,供电厂P又该建在何处能使所用电线最短呢?画出图形,不写作法,保留作图痕迹;
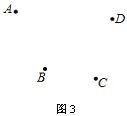
(3)A、B、C、D如图3,连接AC并延长到E,使CE=AC,连接BD并反向延长到F,不写作法,保留作图痕迹.
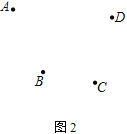
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分) 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分. 如图,甲 在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式
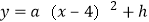 ,已知点O与球网的水平距离为5m,球网的高度1.55m.
,已知点O与球网的水平距离为5m,球网的高度1.55m.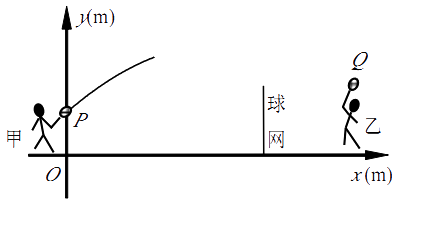
(1)当a=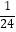 时,①求h的值.②通过计算判断此球能否过网.
时,①求h的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为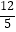 m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某地,人们发现某种蟋蟀1min,所叫次数x与当地温度T之间的关系或为T=ax+b,下面是蟋蟀所叫次数与温度变化情况对照表:
蟋蟀叫的次数(x)
…
84
98
119
…
温度(℃)T
…
15
17
20
…
①根据表中的数据确定a、b的值.
②如果蟋蟀1min叫63次,那么该地当时的温度约为多少摄氏度?
相关试题

