【题目】(1)如图1所示,在正方形ABCD中,对角线AC与BD相交于点O,请填空:![]() = (直接写出答案);
= (直接写出答案);
(2)如图2所示,将(1)中的△BOC绕点B逆时针旋转得到△BO1C1,连接AO1,DC1,请你猜想线段AO1与DC1之间的数量关系,并证明之;
(3)如图3所示,矩形ABCD和Rt△BEF有公共顶点B,且∠BEF=90°,∠EBF=∠ABD=30°,则![]() 的值是否为定值?若是定值,请求出该值;若不是定值,请简述理由.
的值是否为定值?若是定值,请求出该值;若不是定值,请简述理由.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() (3)
(3)![]()
![]()
【解析】
试题分析:(1)根据正方形的性质和等腰直角三角形的性质计算即可;
(2)根据旋转变换的性质得到∠ABO=∠O1B,C1,根据正方形的性质得到![]() ,证明△ABO1∽△DBC1,根据相似三角形的性质解答;
,证明△ABO1∽△DBC1,根据相似三角形的性质解答;
(3)根据正弦的定义和矩形的性质证明△AEB∽△DFB,根据相似三角形的性质计算即可.
试题解析:(1)∵四边形ABCD是正方形,
∴AD=DC,△AOD是等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
故答案为:![]() ;
;
(2)∵△BOC绕点B逆时针旋转得到△BO1C1,
∴∠ABO=∠O1B,C1,
∴∠ABO1=∠DBC1,
∵四边形ABCD是正方形,
∴![]() ,又
,又![]() ,
,
∴![]() ,又∠ABO1=∠DBC1,
,又∠ABO1=∠DBC1,
∴△ABO1∽△DBC1,
∴![]() ;
;
(3)在Rt△EBF中,∠EBF=30°,
∴![]() =
=![]() ,
,
在Rt△ABD中,∠ABD=30°,
∴![]() ,
,
∴![]() ,
,
∵∠EBF=∠ABD,
∴∠EBA=∠FBD,
∴△AEB∽△DFB,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,CD是边AB上的高,且
 .
.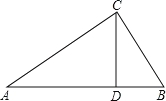
(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a﹣b=1,则2﹣a+b的值是( )
A. 3 B. ﹣1 C. ﹣2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正多边形的边长与半径相等,则这个正多边形的中心角是( )
A.45°B.60°C.72°D.90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多项式加上﹣3x+x﹣2x2得到x2﹣1,那么这个多项式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】按图填空,并注明理由.
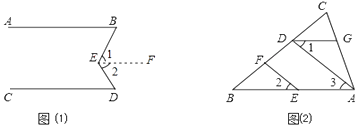
(1)完成正确的证明:如图(1),已知AB∥CD,求证:∠BED=∠B+∠D
证明:过E点作EF∥AB(经过直线外一点有且只有一条直线与这条直线平行)
∴∠1=()
∵AB∥CD(已知)
∴EF∥CD(如果两条直线与同一直线平行,那么它们也平行)
∴∠2=()
又∠BED=∠1+∠2
∴∠BED=∠B+∠D (等量代换).
(2)如图(2),在△ABC中,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:因为EF∥AD(已知)
所以∠2=∠3.()
又因为∠1=∠2,所以∠1=∠3.(等量代换)
所以AB∥()
所以∠BAC+=180° ().
又因为∠BAC=70°,所以∠AGD=110°. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC内接于⊙O,BC为直径,AB=8,AC=6,D是弧AB的中点,CD与AB的交点为E,则
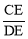 等于( )
等于( )
A.4.8
B.3.5
C.3
D.2.5
相关试题

