【题目】如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门BC打开的宽度为2米,以下哪辆车可以通过?( )
(栏杆宽度,汽车反光镜忽略不计)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.车辆尺寸:长×宽×高)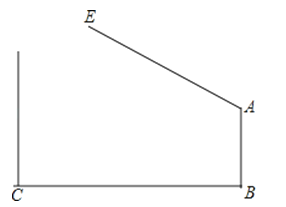
A.宝马Z4(4200mm×1800mm×1360mm)
B.奇瑞QQ(4000mm×1600mm×1520mm)
C.大众朗逸(4600mm×1700mm×1400mm)
D.奥迪A4(4700mm×1800mm×1400mm)
参考答案:
【答案】C
【解析】解:如图,过点A作BC的平行线AG,过点N作NQ⊥BC于Q,交AG于点R,
则∠BAG=90°,
∵∠BAE=127°,∠BAG=90°,
∴∠EAH=∠EAB﹣∠BAG=37°.
在△NAR中,∠ARN=90°,∠EAG=37°,
当车宽为1.8m,则GR=1.8m,故AR=2﹣1.8=0.2(m),
∴NR=ARtan37°=0.2×0.75=0.15(m),
∴NQ=1.2+0.15=1.35<1.36,
∴宝马Z4(4200mm×1800mm×1360mm)无法通过,
∴奥迪A4(4700mm×1800mm×1400mm)无法通过,
故此选项A,D不合题意;
当车宽为1.6m,则GR=1.6m,故AR=2﹣1.6=0.4(m),
∴NR=ARtan37°=0.4×0.75=0.3(m),
∴NQ=1.2+0.3=1.5<1.52,
∴奇瑞QQ(4000mm×1600mm×1520mm)无法通过,故此选项不合题意;
当车宽为1.7m,则GR=1.7m,故AR=2﹣1.7=0.3(m),
∴NR=ARtan37°=0.3×0.75=0.225(m),
∴NQ=1.2+0.225=1.425>1.4,
∴大众朗逸(4600mm×1700mm×1400mm)可以通过,故此选项符合题意;
故选:C.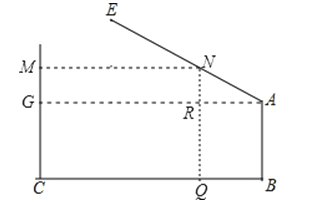
【考点精析】解答此题的关键在于理解解直角三角形的相关知识,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是以AB为直径的⊙O上的一点,BD与过点C的切线互相垂直,垂足为点D.
(1)求证:BC平分∠DBA;
(2)若CD=6,BC=10,求⊙O的半径长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC,交AB于E,则下列结论一定正确的是( )
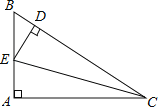
A. AE=BE B. DB=DE C. AE=BD D. ∠BCE=∠ACE
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AB为⊙O的直径,P为AB延长线上的任意一点,过点P作⊙O的切线,切点为C,∠APC的平分线PD与AC交于点D.
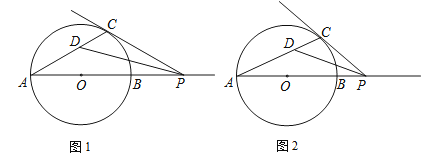
(1)如图1,若∠CPA恰好等于30°,求∠CDP的度数;
(2)如图2,若点P位于(1)中不同的位置,(1)的结论是否仍然成立?说明你的理由. -
科目: 来源: 题型:
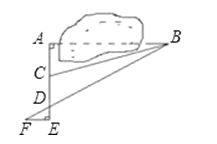
查看答案和解析>>【题目】数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:①AC,∠ACB;②EF、DE、AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A、B两树距离的有( )
A.0组
B.一组
C.二组
D.三组 -
科目: 来源: 题型:
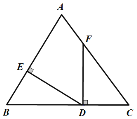
查看答案和解析>>【题目】如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
相关试题

