【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB= ![]() ,反比例函数y=
,反比例函数y= ![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( ) 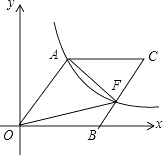
A.60
B.80
C.30
D.40
参考答案:
【答案】D
【解析】解:过点A作AM⊥x轴于点M,如图所示.
设OA=a,
在Rt△OAM中,∠AMO=90°,OA=a,sin∠AOB= ![]() ,
,
∴AM=OAsin∠AOB= ![]() a,OM=
a,OM= ![]() =
= ![]() a,
a,
∴点A的坐标为( ![]() a,
a, ![]() a).
a).
∵点A在反比例函数y= ![]() 的图象上,
的图象上,
∴ ![]() a×
a× ![]() a=
a= ![]() =48,
=48,
解得:a=10,或a=﹣10(舍去).
∴AM=8,OM=6,OB=OA=10.
∵四边形OACB是菱形,点F在边BC上,
∴S△AOF= ![]() S菱形OBCA=
S菱形OBCA= ![]() OBAM=40.
OBAM=40.
故选D.
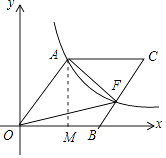
过点A作AM⊥x轴于点M,设OA=a,通过解直角三角形找出点A的坐标,结合反比例函数图象上点的坐标特征即可求出a的值,再根据四边形OACB是菱形、点F在边BC上,即可得出S△AOF= ![]() S菱形OBCA,结合菱形的面积公式即可得出结论.
S菱形OBCA,结合菱形的面积公式即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OA=OB,OC=OD,AD和BC相交于点E,则图中共有全等三角形的对数( )

A. 2对 B. 3对 C. 4对 D. 5对
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四个数:a=
 b=- (-3) , c= -(-1)2019, d=
b=- (-3) , c= -(-1)2019, d= .
.(1) 化简a,b,c,d 得a= ,b= ,c= ,d= ;
(2) 把这四个数在数轴上分别表示出来:

(3)用“<”把 a,b,c,d 连接起来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A、B、C、D是坐标轴上的点且点C坐标是(0,﹣1),AB=5,点(a,b)在如图所示的阴影部分内部(不包括边界),已知OA=OD=4,则a的取值范围是( )
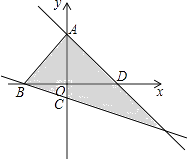
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请完成下面的解答过程.
如图,∠1=∠B,∠C=110°,求∠3的度数.
解:∵∠1=∠B,
∴AD∥ .( )
∴∠C+ =180°.(两直线平行,同旁内角互补)
∵∠C=110°,
∴∠2= °.
∴∠3= =70°.( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,若∠B=130°,OA=1,则
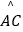 的长为 .
的长为 . 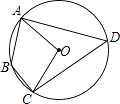
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是A(1,3),B(﹣2,﹣2),C(2,﹣1).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)写出点A1,B1,C1的坐标;
(3)求△ABC的面积.

相关试题

