搜索
【题目】一个等腰三角形的周长为20，一条边的长为6，则其两腰之和为__________.
参考答案：
【答案】12或14
【解析】
已知条件中，没有明确说明已知的边长是否是腰长，所以有两种情况讨论，还应判定能否组成三角形．
解：①底边长为6，则腰长为：（20-6）÷2=7，所以另两边的长为7，7，能构成三角形，7+7=14；
②腰长为6，则底边长为：20-6×2=8，能构成三角形，6+6=12．
故答案为：12或14.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知数轴上点A表示的数为-7，点B表示的数为5，点C到点A，点B的距离相等，动点P从点A出发，以每秒2个单位长度的速度沿数轴向右匀速运动，设运动的时间为
（
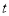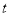＞0）秒（1）点C表示的数是_________
（2）求当
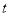等于多少秒时，点P到达点B处（3）点P表示的数是_________（用含有
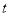的代数式表示）（4）求当t等于多少秒时，PC之间的距离为2个单位长度
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，OABC是平行四边形，对角线OB在y轴正半轴上，位于第一象限的点A和第二象限的点C分别在双曲线
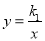和
的一支上，分别过点A、C作x轴的垂线，垂足分别为M和N，则有以下的结论：①
；②阴影部分面积是
（k1+k2）；③当∠AOC=90°时，|k1|=|k2|；④若OABC是菱形，则两双曲线既关于x轴对称，也关于y轴对称．其中正确的结论是（ ）
A．①②③ B．②④ C．①③④ D．①④
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，⊙O的半径为4，B是⊙O外一点，连接OB，且OB=6，过点B作⊙O的切线BD，切点为D，延长BO交⊙O于点A，过点A作切线BD的垂线，垂足为C．
（1）求证：AD平分∠BAC；
（2）求AC的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了解某中学九年级学生中考体育成绩情况，现从中抽取部分学生的体育成绩进行分段（A：50分、B：49～40分、C：39～30分、D：29～0分）统计，统计结果如图所示．
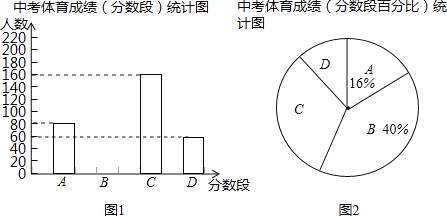
根据上面提供的信息，回答下列问题：
（1）本次抽查了多少名学生的体育成绩；
（2）补全图9.1，求图9.2中D分数段所占的百分比；
（3）已知该校九年级共有900名学生，请估计该校九年级学生体育成绩达到40分以上（含40分）的人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】人在运动时每分钟心跳的次数通常和人的年龄有关，如果用
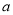表示一个人的年龄，用
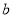表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数，那么
(1)正常情况下，在运动时一个20岁的人所能承受的每分钟心跳的最高次数是多少？
(2)一个50岁的人运动时10秒心跳的次数为23，请问他有危险吗？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，抛物线y=x2﹣2x+k与x轴交于A、B两点，与y轴交于点C（0，﹣3）．[图2、图3为解答备用图]
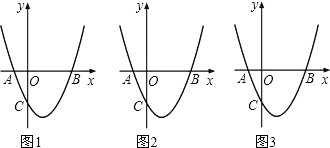
（1）k= ，点A的坐标为 ，点B的坐标为 ；
（2）设抛物线y=x2﹣2x+k的顶点为M，求四边形ABMC的面积；
（3）在x轴下方的抛物线上是否存在一点D，使四边形ABDC的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由；
（4）在抛物线y=x2﹣2x+k上求点Q，使△BCQ是以BC为直角边的直角三角形．
相关试题
