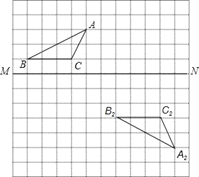
【题目】在如图所示的方格纸中,
(1)作出△ABC关于MN对称的图形△A1B1C1.
(2)说明△A2B2C2可以由△A1B1C1经过怎样的平移变换得到?
(3)以MN所在直线为x轴,AA1的中点为坐标原点,建立直角坐标系xOy,试在x轴上找一点P,使得PA1+PB2最小,直接写出点P的坐标.
参考答案:
【答案】(1)见解析;(2)△A2B2C2可以由△A1B1C1向右平移6个单位,向下平移2个单位得到;(3)作图见解析,点P的坐标为(1,0).
【解析】
(1)依据轴对称的性质,即可得到△ABC关于MN对称的图形△A1B1C1;
(2)依据△A2B2C2与△A1B1C1的位置,即可得到平移的方向和距离;
(3)连接AB2,交x轴于P,连接A1P,依据两点之间,线段最短,即可得到PA1+PB2最小,进而得到点P的坐标.
解:(1)如图所示,△A1B1C1即为所求;
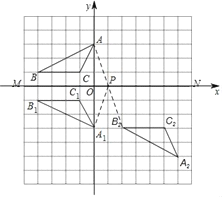
(2)△A2B2C2可以由△A1B1C1向右平移6个单位,向下平移2个单位得到;
(3)如图,连接AB2,交x轴于P,连接A1P,则PA1+PB2最小,
此时,点P的坐标为(1,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.
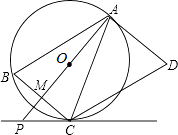
(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若AB=9,BC=6.求PC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A,B两点,抛物线y=﹣x2+bx+c过A,B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.
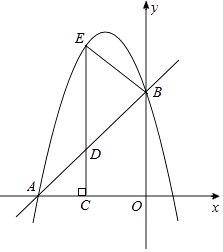
(1)求抛物线的解析式.
(2)求△ABE面积的最大值.
(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求出点D坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣x+1与x轴,y轴分别交于B,A两点,动点P在线段AB上移动,以P为顶点作∠OPQ=45°交x轴于点Q.

(1)求点A和点B的坐标;
(2)比较∠AOP与∠BPQ的大小,说明理由.
(3)是否存在点P,使得△OPQ是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.
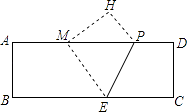
(1)求MP的值;
(2)在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF的周长最小?
(3)若点G,Q是AB边上的两个动点,且不与点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(3﹣m,m﹣1)在第二象限,则m的取值范围在数轴上表示正确的是( )
A.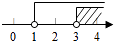
B.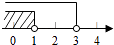
C.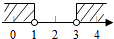
D.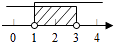
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠CDA.
(1)求证:BE∥DF;
(2)若∠ABC=56°,求∠ADF的大小.

相关试题

