【题目】从甲、乙、丙3名同学中随机选调学生做环保志愿者,求下列事件的概率:
(1)选调1名,恰好是甲;
(2)选调2名,甲在其中.
参考答案:
【答案】(1)抽取1名,恰好是甲的概率为![]() ;
;
(2)抽取2名,甲在其中的概率为![]() .
.
【解析】
试题分析:(1)由从甲、乙、丙3名同学中随机抽取环保志愿者,直接利用概率公式求解即可求得答案;
(2)利用列举法可得抽取2名,可得:甲乙,甲丙,乙丙,共3种等可能的结果,甲在其中的有2种情况,然后利用概率公式求解即可求得答案
试题解析:解:(1)∵从甲、乙、丙3名同学中随机抽取环保志愿者,
∴抽取1名,恰好是甲的概率为![]() ;
;
(2)∵抽取2名,可得:甲乙,甲丙,乙丙,共3种等可能的结果,甲在其中的有2种情况,
∴抽取2名,甲在其中的概率为![]() .
.
-
科目: 来源: 题型:
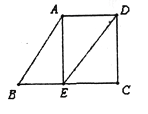
查看答案和解析>>【题目】如图,已知AB∥DE,∠B=60°,AE⊥BC,垂足为点E.
(1)求∠AED的度数;
(2)当∠EDC满足什么条件时,AE∥DC,证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了抓住市文化艺术节的商机,某商店决定购进A,B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,
B种纪念品6件,需要800元.
(1)求购进A,B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某公司计划用32m长的材料沿墙建造的长方形仓库,仓库的一边靠墙,已知墙长16m,设长方形的宽AB为xm.

(1)用x的代数式表示长方形的长BC;
(2)能否建造成面积为120㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由;
(3)能否建造成面积为160㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由.
-
科目: 来源: 题型:
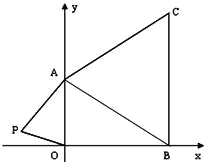
查看答案和解析>>【题目】如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式
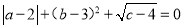
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,
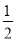 ),请用含m的式子表示四边形ABOP的面积;
),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积为△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象经过点(﹣1,4),且与直线y=﹣x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
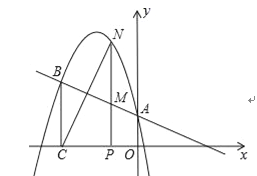
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)在(2)的条件下,是否存在点N,使得BM与NC相互垂直平分?若存在,求出所有满足条件的N点的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用等式的性质解方程的步骤:
(1)利用等式的性质________,方程两边同时加(或减)同一个数(或式子)使一元一次方程左边是________,右边是________;
(2)利用等式的性质________,方程两边同时乘未知数的系数的________,使未知数的系数化为1.
相关试题

