【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=![]() ,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.
,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.
(1)求抛物线的解析式;
(2)填空:
①用含m的式子表示点C,D的坐标:
C( , ),D( , );
②当m= 时,△ACD的周长最小;
(3)若△ACD为等腰三角形,求出所有符合条件的点P的坐标.
参考答案:
【答案】
(1)
解:(1)依题意,得 ,解得
,解得
∴y=x2﹣![]() x
x
(2)m;![]() ;2m;0;1
;2m;0;1
(3)
依题意,得B(m,0)
在RT△OBC中,OC2=OB2+BC2=m2+![]() =
=![]() m2,
m2,
∴OC=![]() m 又∵O,D关于直线PC对称,
m 又∵O,D关于直线PC对称,
∴CD=OC=![]() m
m
在RT△AOE中,OA=![]() =
=![]() =
=![]()
∴AC=OA﹣OC=![]() ﹣
﹣![]() m
m
在RT△ADE中,AD2=AE2+DE2=12+(2﹣2m)2=4m2﹣8m+5
分三种情况讨论:
①若AC=CD,即![]() ﹣
﹣![]() m=
m=![]() m,解得m=1,∴P(1,
m,解得m=1,∴P(1,![]() )
)
②若AC=AD,则有AC2=AD2,即5﹣5m+![]() m2=4m2﹣8m+5
m2=4m2﹣8m+5
解得m1=0,m2=![]() .∵0<m<2,∴m=
.∵0<m<2,∴m=![]() ,∴P(
,∴P(![]() ,
,![]() )
)
③若DA=DC,则有DA2=DC2,即4m2﹣8m+5=![]() m2
m2
解得m1=![]() ,m2=2,∵,0<m<2,∴m=
,m2=2,∵,0<m<2,∴m=![]() ,∴P(
,∴P(![]() ,
,![]() )
)
综上所述,当△ACD为等腰三角形是,点P的坐标分别为P1(1,![]() ),P2(
),P2(![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() ).
).
【解析】(1)根据抛物线对称轴公式和代入法可得关于a,b的方程组,解方程组可得抛物线的解析式;
(2)①设OA所在的直线解析式为y=kx,将点A(2,1)代入求得OA所在的解析式为y=![]() x,因为PC⊥x轴,所以C得横坐标与P的横坐标相同,为m,令x=m,则y=
x,因为PC⊥x轴,所以C得横坐标与P的横坐标相同,为m,令x=m,则y=![]() m,所以得出点C(m,
m,所以得出点C(m,![]() m),又点O、D关于直线PB的对称,所以由中点坐标公式可得点D的横坐标为2m,则点D的坐标为(2m,0);
m),又点O、D关于直线PB的对称,所以由中点坐标公式可得点D的横坐标为2m,则点D的坐标为(2m,0);
②因为O与D关于直线PB的对称,所以PB垂直平分OD,则CO=CD,因为,△ACD的周长=AC+CD+AD=AC+CO+AD=AO,OA=![]() =
=![]() =
=![]() ,所以当AD最小时,△ACD的周长最小;根据垂线段最短,可知此时点D与E重合,其横坐标为2,故m=1.
,所以当AD最小时,△ACD的周长最小;根据垂线段最短,可知此时点D与E重合,其横坐标为2,故m=1.
(3)由中垂线得出CD=OC,再将OC、AC、AD用m表示,然后分情况讨论分别得到关于m的方程,解得m,再根据已知条件选取复合体艺的点P坐标即可.
【考点精析】通过灵活运用二次函数的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现正是闽北特产杨梅热销的季节,某水果零售商店分两批次从批发市场共购进杨梅40箱,已知第一、二次进货价分别为每箱50元、40元,且第二次比第一次多付款700元.
(1)设第一、二次购进杨梅的箱数分别为a箱、b箱,求a,b的值;
(2)若商店对这40箱杨梅先按每箱60元销售了x箱,其余的按每箱35元全部售完.
①求商店销售完全部杨梅所获利润y(元)与x(箱)之间的函数关系式;
②当x的值至少为多少时,商店才不会亏本.
(注:按整箱出售,利润=销售总收入﹣进货总成本) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=3
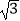 ﹣3,CD∥AB,并与弧AB相交于点M、N.
﹣3,CD∥AB,并与弧AB相交于点M、N. 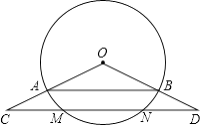
(1)求线段OD的长;
(2)若sin∠C= ,求弦MN的长;
,求弦MN的长;
(3)在(2)的条件下,求优弧MEN的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB=18米,
 于点A,MA=6米,射线
于点A,MA=6米,射线 于点B,P点从B点出发向A运动,每秒走1米,Q点从B点向D点运动,每秒走2米,P,Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
于点B,P点从B点出发向A运动,每秒走1米,Q点从B点向D点运动,每秒走2米,P,Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
A. 4 B. 6 C. 4或9 D. 6或9
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2﹣2bx+c
(1)若抛物线的顶点坐标为(2,﹣3),求b,c的值;
(2)若b+c=0,是否存在实数x,使得相应的y的值为1,请说明理由;
(3)若c=b+2且抛物线在﹣2≤x≤2上的最小值是﹣3,求b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD中,AD∥BC,∠BAD=90°,CE⊥AD于点E,AD=8cm,BC=4cm,AB=5cm.从初始时刻开始,动点P,Q 分别从点A,B同时出发,运动速度均为1cm/s,动点P沿A﹣B﹣﹣C﹣﹣E的方向运动,到点E停止;动点Q沿B﹣﹣C﹣﹣E﹣﹣D的方向运动,到点D停止,设运动时间为xs,△PAQ的面积为ycm2 , (这里规定:线段是面积为0的三角形)

解答下列问题:
(1)当x=2s时,y=cm2;当x= s时,y=cm2 .
s时,y=cm2 .
(2)当5≤x≤14 时,求y与x之间的函数关系式.
(3)当动点P在线段BC上运动时,求出 S梯形ABCD时x的值.
S梯形ABCD时x的值.
(4)直接写出在整个运动过程中,使PQ与四边形ABCE的对角线平行的所有x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中是真命题的是( )
A.经过直线外一点,有且仅有一条直线与一线与已知直线垂直
B.平分弦的直径垂直于弦
C.对角线互相平分且垂直的四边形是菱形
D.反比例函数y=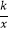 ,当k<0时,y随x的增大而增大
,当k<0时,y随x的增大而增大
相关试题

