搜索
【题目】如图，已知线段AB=18米，
于点A，MA=6米，射线
于点B，P点从B点出发向A运动，每秒走1米，Q点从B点向D点运动，每秒走2米，P，Q同时从B出发，则出发x秒后，在线段MA上有一点C，使△CAP与△PBQ全等，则x的值为（ ）
A. 4 B. 6 C. 4或9 D. 6或9
参考答案：
【答案】B
【解析】
分两种情况考虑：当△APC≌△BQP时与当△APC≌△BPQ时，根据全等三角形的性质即可确定出时间．
当△APC≌△BQP时，AP=BQ，即18x=2x，
解得：x=6；
当△APC≌△BPQ时,AP=BP=12AB=9米，
此时所用时间为9秒，AC=BQ=18米，不合题意，舍去；
综上，出发6秒后，在线段MA上有一点C，使△CAP与△PBQ全等.
故选B.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在我市实施“城乡环境综合治理”期间，某校组织学生开展“走出校门，服务社会”的公益活动．八年级一班王浩根据本班同学参加这次活动的情况，制作了如下的统计图表： 该班学生参加各项服务的频数、频率统计表：
服务类别
频数
频率
文明宣传员
4
0.08
文明劝导员
10
义务小警卫
8
0.16
环境小卫士
0.32
小小活雷锋
12
0.24
请根据上面的统计图表，解答下列问题：
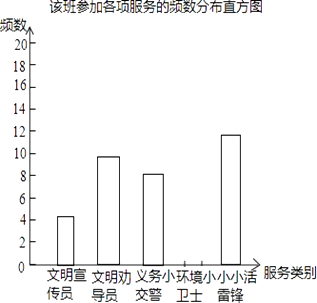
（1）该班参加这次公益活动的学生共有名；
（2）请补全频数、频率统计表和频数分布直方图；
（3）若八年级共有900名学生报名参加了这次公益活动，试估计参加文明劝导的学生人数． -
科目： 来源： 题型：
查看答案和解析>>【题目】现正是闽北特产杨梅热销的季节，某水果零售商店分两批次从批发市场共购进杨梅40箱，已知第一、二次进货价分别为每箱50元、40元，且第二次比第一次多付款700元．
（1）设第一、二次购进杨梅的箱数分别为a箱、b箱，求a，b的值；
（2）若商店对这40箱杨梅先按每箱60元销售了x箱，其余的按每箱35元全部售完．
①求商店销售完全部杨梅所获利润y（元）与x（箱）之间的函数关系式；
②当x的值至少为多少时，商店才不会亏本．
（注：按整箱出售，利润=销售总收入﹣进货总成本） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点C、D分别在扇形AOB的半径OA、OB的延长线上，且OA=3，AC=3
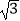﹣3，CD∥AB，并与弧AB相交于点M、N．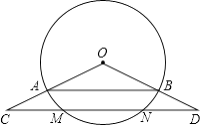 
（1）求线段OD的长；
（2）若sin∠C=
，求弦MN的长；
（3）在（2）的条件下，求优弧MEN的长度． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知抛物线y=ax2+bx的对称轴为x=
，且经过点A（2，1），点P是抛物线上的动点，P的横坐标为m（0＜m＜2），过点P作PB⊥x轴，垂足为B，PB交OA于点C，点O关于直线PB的对称点为D，连接CD，AD，过点A作AE⊥x轴，垂足为E．
（1）求抛物线的解析式;
（2）填空：
①用含m的式子表示点C，D的坐标：
C（ ， ），D（ ， ）；
②当m= 时，△ACD的周长最小；
（3）若△ACD为等腰三角形，求出所有符合条件的点P的坐标. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=x2﹣2bx+c
（1）若抛物线的顶点坐标为（2，﹣3），求b，c的值；
（2）若b+c=0，是否存在实数x，使得相应的y的值为1，请说明理由；
（3）若c=b+2且抛物线在﹣2≤x≤2上的最小值是﹣3，求b的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，梯形ABCD中，AD∥BC，∠BAD=90°，CE⊥AD于点E，AD=8cm，BC=4cm，AB=5cm．从初始时刻开始，动点P，Q 分别从点A，B同时出发，运动速度均为1cm/s，动点P沿A﹣B﹣﹣C﹣﹣E的方向运动，到点E停止；动点Q沿B﹣﹣C﹣﹣E﹣﹣D的方向运动，到点D停止，设运动时间为xs，△PAQ的面积为ycm2 ， （这里规定：线段是面积为0的三角形）
解答下列问题：
（1）当x=2s时，y=cm2；当x=
s时，y=cm2 ．
（2）当5≤x≤14 时，求y与x之间的函数关系式．
（3）当动点P在线段BC上运动时，求出
S梯形ABCD时x的值．
（4）直接写出在整个运动过程中，使PQ与四边形ABCE的对角线平行的所有x的值．
相关试题
