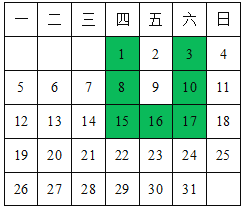
【题目】如图,表中给出的是某月的月历,任意选取“U”型框中的7个数(如阴影部分所示),请你运用所学的数学知识来研究,发现这7个数的和不可能的是( )
A.70B.78C.84D.![]()
参考答案:
【答案】B
【解析】
设“U”型框中的正中间的数为x,则其他6个数分别为x15,x13,x8,x-6,x-1,x+1,表示出这7个数之和,然后分别列出方程解答即可.
设“U”型框中的正中间的数为x,则其他6个数分别为x15,x13,x8,x-6,x-1,x+1,
这7个数之和为:x15+x13+x8+x-6+x-1+x+1+x=7x-42.
由题意得
A、7x-42=70,解得:x=16,能求得这7个数;
B、7x-42=78,解得:x=![]() ,不能求得这7个数;
,不能求得这7个数;
C、7x-42=84,解得:x=18,能求得这7个数;
D、7x-42=105,解得:x=21,能求得这7个数.
故选:B.
-
科目: 来源: 题型:
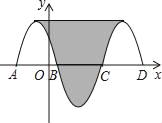
查看答案和解析>>【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B的中心对称得C2,C2与x轴交于另一点C,将C2关于点C的中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为_____.
【答案】32
【解析】试题分析:∵抛物线y=﹣x2﹣2x+3与x轴交于点A、B,
∴当y=0时,则﹣x2﹣2x+3=0,
解得x=﹣3或x=1,
则A,B的坐标分别为(﹣3,0),(1,0),
AB的长度为4,
从C1,C3两个部分顶点分别向下作垂线交x轴于E、F两点.
根据中心对称的性质,x轴下方部分可以沿对称轴平均分成两部分补到C1与C2.
如图所示,阴影部分转化为矩形.
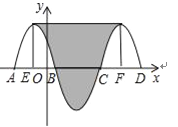
根据对称性,可得BE=CF=4÷2=2,则EF=8
利用配方法可得y=﹣x2﹣2x﹣3=﹣(x+1)2+4
则顶点坐标为(﹣1,4),即阴影部分的高为4,
S阴=8×4=32.
考点:抛物线与x轴的交点.
【题型】填空题
【结束】
17【题目】解方程:(1)2(3x﹣1)=16;(2)
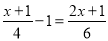 ;(3)
;(3)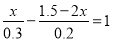 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们在“堆石子”游戏中发现:像图(1)中的
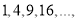 这些数据能够表示成正方形,可将其称为正方形数;类似地,像图(2)中的
这些数据能够表示成正方形,可将其称为正方形数;类似地,像图(2)中的 这些数据能够表示成三角形,可将其称为三角形数.
这些数据能够表示成三角形,可将其称为三角形数.
(1)第
 个正方形数是 ;第
个正方形数是 ;第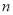 个正方形数是 ;
个正方形数是 ;(2)第
 个三角形数是 ;第
个三角形数是 ;第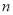 个三角形数是 ;
个三角形数是 ;(3)若将一堆小石子按一定规律摆成下列图形,请求出第
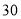 个图形中“●”的个数.
个图形中“●”的个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
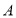 在数轴上对应的数为
在数轴上对应的数为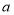 ,点
,点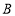 对应的数为
对应的数为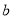 ,且
,且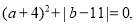 G为线段
G为线段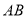 上一点,
上一点,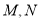 两点分别从
两点分别从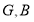 点沿
点沿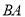 方向同时运动,设
方向同时运动,设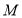 点的运动速度为
点的运动速度为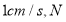 点的运动速度为
点的运动速度为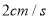 ,运动时间为
,运动时间为 .
.(1)
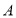 点对应的数为 ,
点对应的数为 ,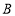 点对应的数为 ;
点对应的数为 ;(2)若
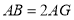 ,试求
,试求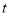 为多少
为多少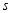 时,
时,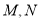 两点的距离为
两点的距离为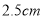 ;
;(3)若
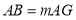 ,点
,点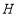 为数轴上任意一点,且
为数轴上任意一点,且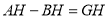 ,请直接写出
,请直接写出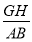 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某村庄计划建造A,B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积和可供使用农户数见下表:
型号
占地面积
(单位:m2/个)
可供使用农户数
(单位:户/个)
A
15
18
B
20
30
已知可供建造沼气池的占地面积不超过365m2,该村农户共有492户.
(1)如何合理分配建造A,B型号“沼气池”的个数才能满足条件?满足条件的方案有几种?通过计算分别写出各种方案.
(2)请写出建造A、B两种型号的“沼气池”的总费用y和建造A型“沼气池”个数x之间的函数关系式;
(3)若A型号“沼气池”每个造价2万元,B型号“沼气池”每个造价3万元,试说明在(1)中的各种建造方案中,哪种建造方案最省钱,最少的费用需要多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
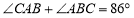 ,
,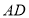 平分
平分 ,与
,与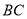 边交于点
边交于点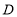 ,
,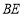 平分
平分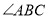 ,与
,与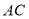 边交于点
边交于点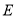 .
.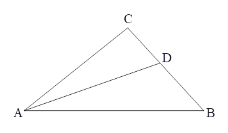
(1)依题意补全图形,并猜想
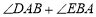 的度数等于 ;
的度数等于 ;(2)填空,补全下面的证明过程.
∵
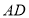 平分
平分 ,
,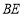 平分
平分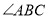 ,
,∴
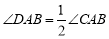 ,
,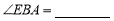 .(理由: )
.(理由: )∵
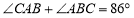 ,
,∴
 ______
______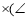 _________
_________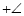 _________
_________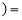 _____
_____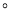 .
.
相关试题

